题目内容
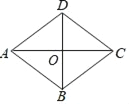
【题目】如图,已知四边形ABCD是平行四边形,对角线AC与BD相交于点O,且对角线AC平分∠BCD,∠ACD=30°,BD=6.
(1)求证:△BCD是等边三角形;(2)求AC的长(结果保留根号).
【答案】(1)见解析;(2)AC的长为6![]() .
.
【解析】
(1)先证四边形ABCD是菱形,得BC=CD,即已知两边相等,再寻找一个角为60°,即可证明△BCD是等边三角形;
(2)先由三角函数求OC的长,即可得出AC的长.
(1)∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,∴∠DAC=∠BCA,∠BAC=∠DCA.
∵AC平分∠BCD,∴∠ACD=∠ACB,∴∠ACD=∠CAD,∴AD=CD,∴四边形ABCD是菱形,∴BC=CD.
∵∠ACD=30°,∴∠BCD=60°,∴△BCD是等边三角形.
(2)∵O为菱形对角线的交点,∴AC=2OC,OD![]() BD=3,∠COD=90°.
BD=3,∠COD=90°.
在Rt△COD中,![]() tan∠OCD=tan30°,∴OC
tan∠OCD=tan30°,∴OC![]() ,∴AC=2OC=6
,∴AC=2OC=6![]() .
.
答:AC的长为6![]() .
.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目