题目内容
【题目】根据题意解答
(1)探究:如图①,在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,AE⊥CD于点E,若AE=8,求四边形ABCD的面积. 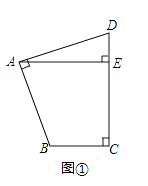
(2)应用:如图②,在四边形ABCD中,∠ABC+∠ADC=180°,AB=AD,AE⊥BC于点E,若AE=20,BC=10,CD=6,则四边形ABCD的面积为 . 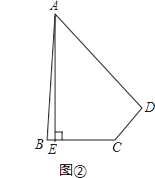
【答案】
(1)解:探究:如图1,过A作AF⊥BC,交CB的延长线于F,
∵AE⊥CD,∠C=90°
∴∠AED=∠F=∠C=90°,
∴四边形AFCE是矩形,
∴∠FAE=90°,
∵∠DAB=90°,
∴∠DAE=∠BAF=90°﹣∠BAE,
在△AFB和△AED中, 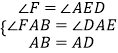 ,
,
∴△AFB≌△AED(AAS),
∴AE=AF=8,S△AFB=S△AED,
∵四边形AFCE是矩形,
∴四边形AFCE是正方形,
∴S正方形AFCE=8×8=64,
∴S四边形ABCD
=S四边形ABCE+S△AED
=S四边形ABCE+S△AFB
=S正方形AFCE
=64;
(2)160
【解析】(2)应用:如图2,过A作AF⊥CD,交CD的延长线于F, ∵AE⊥CD,
∴∠AED=∠F=90°,
∴∠FAE+∠BCD=180°,
∵∠ABC+∠ADC=180°,
∴∠BAD+∠BCD=180°,
∴∠BAD=∠EAF,
∴∠BAD﹣∠EAD=∠EAF﹣∠EAD,
∴∠BAE=∠FAD,
在△AEB和△AFD中,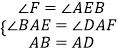 ,
,
∴△AEB≌△AFD(AAS),
∴AE=AF=19,BE=DF,
设BE=DF=x,
∵BC=10,CD=6,
∴CE=10﹣x,CF=6+x,
由勾股定理得;AC2=AE2+CE2=AF2+CF2 ,
∵AE=AF,
∴CE=CF,
即10﹣x=6+x,
解得:x=2,
∴CE=CF=8,
∵△AEB≌△AFD
∴S△AEB=S△AFD ,
∴S正方形AFCE= ![]() ×8×20+
×8×20+ ![]() ×8×20=160.
×8×20=160.
∴S四边形ABCD
=S△AEB+S四边形AECD
=S△AFD+S四边形AECD
=S正方形AFCE
=160.
所以答案是:160.

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案