题目内容
【题目】已知:如图,点E、F、G、H分别在菱形ABCD的各边上,且AE=AH=CF=CG.
(1)求证:四边形EFGH是矩形;
(2)若AB=6,∠A=60°.
①设BE=x,四边形EFGH的面积为S,求S与x之间的函数表达式;
②x为何值时,四边形EFGH的面积S最大?并求S的最大值.

【答案】(1)证明见解析(2)①![]() ②当
②当![]() 时,四边形的面积最大为
时,四边形的面积最大为![]()
【解析】分析:(1)、首先利用菱形的性质得到∠A=∠C,∠B=∠D,AB=BC=CD=DA,然后根据AE=AH=CF=CG,得到BE=BF=DH=DG,从而证得△AEH≌△CGF,△BEF≌△DGH,证得四边形EFGH是平行四边形,然后利用有一个角是直角的平行四边形是矩形判定四边形EFGH是矩形;(2)、①过点B作BN⊥EF于点N,根据题意得出NE和EF的长度,然后根据∠A=60°,AE=AH得出△AEH为等边三角形,从而得出函数关系式;②根据二次函数的性质求出面积的最大值.
详解:(1)、∵四边形ABCD是菱形, ∴![]() .
.
∵![]() , ∴
, ∴![]() . ∴
. ∴![]() . 同理:
. 同理:![]() .
.
所以四边形![]() 是平行四边形. 又∵
是平行四边形. 又∵![]() , ∴
, ∴![]() .
.
∴![]() . ∵
. ∵![]() , ∴
, ∴![]() .
.
∵![]() ,
,
∴![]() . ∴
. ∴![]() . ∴
. ∴![]() .
.
∴四边形![]() 是矩形.
是矩形.
(2)、①过点B作BN⊥EF于点N,根据题意可得:NE=![]() . ∴
. ∴![]() ,∵
,∵![]() ,
,
∴![]() 是等边三角形. ∴
是等边三角形. ∴![]() , ∴
, ∴![]() .
.
②![]() . 当
. 当![]() 时,
时,![]() .
.
所以当![]() 时,四边形的面积最大为
时,四边形的面积最大为![]() .
.
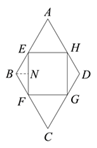

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目