题目内容
如图1,O为圆柱形木块底面的圆心,过底面的一条弦AD,沿母线 AB剖开,得剖面矩形ABCD,AD=24cm,AB=25cm.若
AB剖开,得剖面矩形ABCD,AD=24cm,AB=25cm.若 |
| AmD |
| 2 |
| 3 |
(1)求⊙O的半径;
(2)求这个圆柱形木块的表面积.(结果可保留π和根号)
分析:(1)根据
的长为底面周长的
,可将扇形的圆心角求出,再根据弦AD的长可将⊙O的半径求出;
(2)圆柱形木块的表面积S=2S圆+S侧,将上下两个圆的面积和侧面的面积求出,相加即可.
 |
| AmD |
| 2 |
| 3 |
(2)圆柱形木块的表面积S=2S圆+S侧,将上下两个圆的面积和侧面的面积求出,相加即可.
解答: 解:(1)如图:连接OA,OD,过O作OE⊥AD,垂足为E,
解:(1)如图:连接OA,OD,过O作OE⊥AD,垂足为E,
∵
由已知的长=
圆周长,
∴扇形OAmD的圆心角为360°×
=240°.
∠AOD=360°-240°=120°.
∵OE⊥AD,
∴∠AOE=
×120°=60°,AE=
AD.
∵AD=24cm,
∴AE=12cm.
在Rt△AOE中,sin∠AOE=
,
∴AO=
=12÷
=8
(cm).
即⊙O的半径为8
cm.
(2)设圆柱的表面积为S,则S=2S圆+S侧,
2S圆=2π×(8
)2=384π(cm2),
S侧=2π×8
×25=400
π(cm2),
∴S=(384+400
)πcm2
答:木块的表面积为(384+400
)πcm2.
 解:(1)如图:连接OA,OD,过O作OE⊥AD,垂足为E,
解:(1)如图:连接OA,OD,过O作OE⊥AD,垂足为E,∵
 |
| AmD |
| 2 |
| 3 |
∴扇形OAmD的圆心角为360°×
| 2 |
| 3 |
∠AOD=360°-240°=120°.
∵OE⊥AD,
∴∠AOE=
| 1 |
| 2 |
| 1 |
| 2 |
∵AD=24cm,
∴AE=12cm.
在Rt△AOE中,sin∠AOE=
| AE |
| AO |
∴AO=
| AE |
| sin60° |
| ||
| 2 |
| 3 |
即⊙O的半径为8
| 3 |
(2)设圆柱的表面积为S,则S=2S圆+S侧,
2S圆=2π×(8
| 3 |
S侧=2π×8
| 3 |
| 3 |
∴S=(384+400
| 3 |
答:木块的表面积为(384+400
| 3 |
点评:本题要求掌握圆柱的有关性质和表面积的求法.

练习册系列答案
相关题目
 ,得剖面矩形ABCD,AD=12cm,AB=15cm.测量出AD所对的圆心角为120°,如图2所示.
,得剖面矩形ABCD,AD=12cm,AB=15cm.测量出AD所对的圆心角为120°,如图2所示. 的长为底面周长的
的长为底面周长的 ,如图2所示.
,如图2所示.
 的长为底面周长的
的长为底面周长的 ,如图2所示.
,如图2所示.
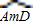 的长为底面周长的
的长为底面周长的 ,如图2所示.
,如图2所示.