题目内容
(2003•杭州)如图,⊙C经过原点且与两坐标轴分别交于A、B两点,点A的坐标是(0,4),M是圆上一点,∠BMO=120°,求⊙C的半径和圆心C的坐标.
【答案】分析:(1)由于∠AOB=90°,那么应连接AB,得到AB是直径.由∠BMO=120°可得到∠BAO=60°,易得OA=4,利用60°的三角函数,即可求得AB,进而求得半径.
(2)利用勾股定理可得OB长,作出OB的弦心距,利用勾股定理可得到C的横坐标的绝对值,同法可得到点C的横坐标.
解答: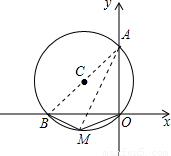 解:(1)连接AB,AM,则由∠AOB=90°,故AB是直径,
解:(1)连接AB,AM,则由∠AOB=90°,故AB是直径,
由∠BAM+∠OAM=∠BOM+∠OBM=180°-120°=60°,
得∠BAO=60°,
又AO=4,故cos∠BAO=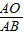 ,AB=
,AB=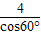 =8,
=8,
从而⊙C的半径为4.
(2)由(1)得,BO=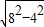 =4
=4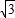 ,
,
过C作CE⊥OA于E,CF⊥OB于F,
则EC=OF= BO=
BO=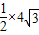 =2
=2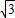 ,CF=OE=
,CF=OE= OA=2.
OA=2.
故C点坐标为(-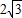 ,2).
,2).
点评:本题用到的知识点为:90°的圆周角所对的弦是直径;圆内接四边形的对角互补.连接90°所对的弦,做弦心距是常用的辅助线方法.
(2)利用勾股定理可得OB长,作出OB的弦心距,利用勾股定理可得到C的横坐标的绝对值,同法可得到点C的横坐标.
解答:
 解:(1)连接AB,AM,则由∠AOB=90°,故AB是直径,
解:(1)连接AB,AM,则由∠AOB=90°,故AB是直径,由∠BAM+∠OAM=∠BOM+∠OBM=180°-120°=60°,
得∠BAO=60°,
又AO=4,故cos∠BAO=
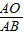 ,AB=
,AB=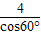 =8,
=8,从而⊙C的半径为4.
(2)由(1)得,BO=
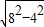 =4
=4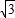 ,
,过C作CE⊥OA于E,CF⊥OB于F,
则EC=OF=
 BO=
BO=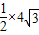 =2
=2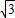 ,CF=OE=
,CF=OE= OA=2.
OA=2.故C点坐标为(-
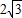 ,2).
,2).点评:本题用到的知识点为:90°的圆周角所对的弦是直径;圆内接四边形的对角互补.连接90°所对的弦,做弦心距是常用的辅助线方法.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目



