题目内容
（2003•杭州）如图，点C为⊙O的弦AB上一点，点P为⊙O上一点，且OC⊥CP，则有（ ）
A．OC2=CA•CB
B．OC2=PA•PB
C．PC2=PA•PB
D．PC2=CA•CB
【答案】分析：延长PC交圆于D，连接OP，OD．根据相交弦定理和垂径定理求解．
解答：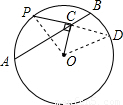
解：延长PC交圆于D，连接OP，OD
根据相交弦定理，得CP•CD=CA•CB
∵OP=OD，OC⊥PC
∴PC=CD
则PC2=CA•CB
故选D．
点评：此题综合运用了相交弦定理以及等腰三角形的三线合一．
解答：
解：延长PC交圆于D，连接OP，OD根据相交弦定理，得CP•CD=CA•CB
∵OP=OD，OC⊥PC
∴PC=CD
则PC2=CA•CB
故选D．
点评：此题综合运用了相交弦定理以及等腰三角形的三线合一．
练习册系列答案
相关题目
