题目内容
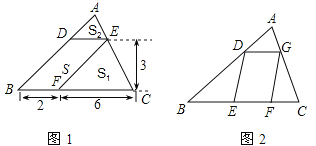
【题目】问题背景:(1)如图1,△ABC中,DE∥BC分别交AB,AC于D,E两点,过点E作EF∥AB交BC于点F。请按图示数据填空:四边形DBFE的面积![]() ______,△EFC的面积
______,△EFC的面积![]() ______,△ADE的面积
______,△ADE的面积![]() ______。
______。
探究发现:(2)在(1)中,若![]() ,
, ![]() ,DE与BC间的距离为
,DE与BC间的距离为![]() 。请证明
。请证明![]() 。
。
拓展迁移:(3)如图2,□DEFG的四个顶点在△ABC的三边上,若△ADG、△DBE、△GFC的面积分别为2、5、3,试利用(2)中的结论求△ABC的面积。
【答案】 6 9 1(2)见解析(3)18
【解析】整体分析:
(1)用面积公式分别求平行四边形DBFE的面积S,△EFC的面积S1,由相似三角形的面积比等于相似比的平方求得△ABC的面积,从而求得△ADE的面积;(2)根据△ADE∽△EFC,分别用a,b,h表示出S1,S2,S的面积可求解;(3)过点G作GH∥AB交BC于点H,由△DBE≌△GHF,得△GHC的面积,由(2)的结论得四边形DBHG的面积.
解:(1)6,9,1
(2)证明:∵DE∥BC,EF∥AB,
∴四边形DBFE为平行四边形,∠AED=∠C,∠A=∠CEF,∴△ADE∽△EFC,
∴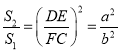 ,∵
,∵![]() ,∴
,∴![]() ,
,
∴![]() ,而S=ah,∴S2=4S1S2;
,而S=ah,∴S2=4S1S2;
(3)解:如图,过点G作GH∥AB交BC于点H,则四边形DBHG为平行四边形,
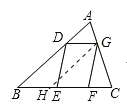
∴∠GHC=∠B,BD=HG,DG=BH,∵四边形DEFG为平行四边形,
∴DG=EF,∴BH=EF,∴BE=HF,
∴△DBE≌△GHF,∴△GHC的面积为5+3=8,
由(2)得,四边形DBHG的面积为![]() ,∴△ABC的面积为2+8+8=18。
,∴△ABC的面积为2+8+8=18。

练习册系列答案
 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目