��Ŀ����
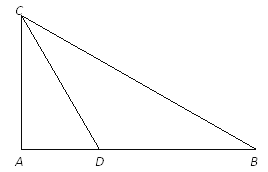
����Ŀ����ͼ��ʾ��������y=ax2+bx+c��a��0����x�ύ�ڵ�A��-2��0����B��1��0����ֱ��x=![]() ��������߽��ڵ�C����x�ύ�ڵ�M����ֱ����ȡ��D��ʹMD=MC������AC��BC��AD��BD��ijͬѧ����ͼ��д�����н��ۣ���a-b=0���ڵ�x��
��������߽��ڵ�C����x�ύ�ڵ�M����ֱ����ȡ��D��ʹMD=MC������AC��BC��AD��BD��ijͬѧ����ͼ��д�����н��ۣ���a-b=0���ڵ�x��![]() ʱ��y��x����������ı���ACBD�����Σ���9a-3b+c��0������Ϊ������ȷ����
ʱ��y��x����������ı���ACBD�����Σ���9a-3b+c��0������Ϊ������ȷ����

A. �ڢۢ� B. �٢ڢ� C. �٢ۢ� D. �٢ڢۢ�
���𰸡�B
����������1����������y=ax2+bx+c��a��0����x�ύ�ڵ�A��-2��0����B��1��0����
��![]() �٣�
�٣�![]() �ڣ�
�ڣ�
���ɢ�-�ڿɵã� ![]() ������
������ ![]() ���ʵ�һ��������ȷ��
���ʵ�һ��������ȷ��
��2���ߵ�A��B������ֱ�Ϊ��-2��0������1��0������M������Ϊ��-0.5��0����
����M���߶�AB���е㣬
��ֱ��![]() �������ߵĶԳ�����
�������ߵĶԳ�����
���������߿���������
����x��![]() ʱ��y��x��������ʵڶ�����������ȷ�ģ�
ʱ��y��x��������ʵڶ�����������ȷ�ģ�
��3���ߵ�M����AB�е㣬����CD�е㣬��CD��AB��
��CD��AB���ഹֱƽ�֣�
���ı���ACBD������.�ʵ�������������ȷ�ģ�
��4���������ߵĿ������£���A�������ǣ�-2��0����
�����ͼ���֪����![]() ��
�� ![]() ���ʵ��ĸ������Ǵ���ģ�
���ʵ��ĸ������Ǵ���ģ�
������������ȷ�Ľ������٢ڢ�.
��ѡB.

 �����Ծ���ĩ���100��ϵ�д�
�����Ծ���ĩ���100��ϵ�д� ˫��ͬ������ѵ��ϵ�д�
˫��ͬ������ѵ��ϵ�д�