题目内容
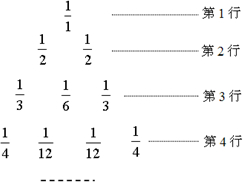 将杨辉三角中的每一个数都换成分数,得到一个如右图所示的分数三角形,称为莱布尼兹三角形.若用有序数对(m,n)表示第m行,从左到右第n个数,如(4,3)表示分数
将杨辉三角中的每一个数都换成分数,得到一个如右图所示的分数三角形,称为莱布尼兹三角形.若用有序数对(m,n)表示第m行,从左到右第n个数,如(4,3)表示分数| 1 | 12 |
分析:根据已知中“莱布尼兹调和三角形”数阵中所示的规律,我们观察、分析、归纳后,可得每一行的第一数均为行数的倒数,且每一个数等于下一行中“脚踩”的两个数的和,由此分别求出第5行、第6行和第7行的第一个数,再求出第6行和第7行的第二个数,进而求出第7行的第3个数.
解答:解:由“莱布尼兹调和三角形”中数的排列规律,
我们可以推断:
第5行的第一个数为:
,
第6行的第一个数为:
,
第7行的第一个数为:
,
则第6行的第二个数为:
-
=
,
第7行的第二个数为:
-
=
,
所以第7行的第三个数为:
-
=
.
故答案为:
.
我们可以推断:
第5行的第一个数为:
| 1 |
| 5 |
第6行的第一个数为:
| 1 |
| 6 |
第7行的第一个数为:
| 1 |
| 7 |
则第6行的第二个数为:
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 30 |
第7行的第二个数为:
| 1 |
| 6 |
| 1 |
| 7 |
| 1 |
| 42 |
所以第7行的第三个数为:
| 1 |
| 30 |
| 1 |
| 42 |
| 1 |
| 105 |
故答案为:
| 1 |
| 105 |
点评:此题考查的知识点是数字的变化类问题,也考查了学生解决实际问题的能力和阅读理解能力,找出本题的数字规律是正确解题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
 将杨辉三角中的每一个数都换成分数,得到一个如图所示的分数三角形,称莱布尼茨三角形.若用有序实数对(m,n)表示第m行,从左到右第n个数,如(4,3)表示分数
将杨辉三角中的每一个数都换成分数,得到一个如图所示的分数三角形,称莱布尼茨三角形.若用有序实数对(m,n)表示第m行,从左到右第n个数,如(4,3)表示分数 .那么(9,2)表示的分数是 .
.那么(9,2)表示的分数是 .
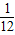 .那么(9,2)表示的分数是 .
.那么(9,2)表示的分数是 .
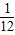 .那么(9,2)表示的分数是 .
.那么(9,2)表示的分数是 .