题目内容
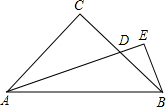 如图所示,在等腰三角形ABC中,∠C=90°,AD是∠BAC的平分线,∠E=90°,那么AD与BE的长度关系为
如图所示,在等腰三角形ABC中,∠C=90°,AD是∠BAC的平分线,∠E=90°,那么AD与BE的长度关系为AD=2BE
AD=2BE
.分析:延长AC,BE交于O,证△ACD≌△BCO,推出AD=BO,证△AEO≌△AEB,推出BE=OE,即可得出答案.
解答:解: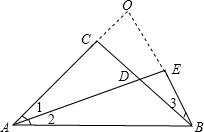 AD=2BE,
AD=2BE,
理由是:延长AC,BE交于O,
∵∠C=∠AEB=90°,∠CDA=∠EDB,
∴由三角形内角和定理得:∠1=∠3,
∵∠ACD=∠BCO=90°,
在△ACD和△BCO中,
,
∴△ACD≌△BCO(ASA),
∴AD=BO,
∵AD平分∠CAB,
∴∠1=∠2,
∵∠AEB=∠AEO=90°,
在△AEO和△AEB中,
,
∴△AEO≌△AEB(ASA),
∴OE=BE,
∴BO=2BE,
∴AD=2BE,
故答案为:AD=2BE.
 AD=2BE,
AD=2BE,理由是:延长AC,BE交于O,
∵∠C=∠AEB=90°,∠CDA=∠EDB,
∴由三角形内角和定理得:∠1=∠3,
∵∠ACD=∠BCO=90°,
在△ACD和△BCO中,
|
∴△ACD≌△BCO(ASA),
∴AD=BO,
∵AD平分∠CAB,
∴∠1=∠2,
∵∠AEB=∠AEO=90°,
在△AEO和△AEB中,
|
∴△AEO≌△AEB(ASA),
∴OE=BE,
∴BO=2BE,
∴AD=2BE,
故答案为:AD=2BE.
点评:本题考查了三角形内角和定理,全等三角形的性质和判定,角平分线定义的应用,主要考查学生的推理能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
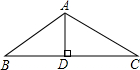 如图所示,在等腰三角形ABC中,AB=AC=12cm,∠ABC=30°,那么底边上的高AD=
如图所示,在等腰三角形ABC中,AB=AC=12cm,∠ABC=30°,那么底边上的高AD= B点,同时点Q以2米/分的速度从点B移动到C点(当一个点到达后全部停止移动).
B点,同时点Q以2米/分的速度从点B移动到C点(当一个点到达后全部停止移动). 如图所示,在等腰三角形ABC中,AB=AC=13cm,底边BC=10cm,求底边上的高AD和△ABC的面积.
如图所示,在等腰三角形ABC中,AB=AC=13cm,底边BC=10cm,求底边上的高AD和△ABC的面积.