题目内容
如图所示,在等腰三角形ABC中,∠B=90°,AB=BC=4米,点P以1米/分的速度从A点出发移动到 B点,同时点Q以2米/分的速度从点B移动到C点(当一个点到达后全部停止移动).
B点,同时点Q以2米/分的速度从点B移动到C点(当一个点到达后全部停止移动).(1)设经过x分钟后,△PCB的面积为y1,△QAB的面积为y2,求出y1,y2关于x的函数关系式;
(2)同时移动多少分钟,这两个三角形的面积相等?
(3)移到时间在什么范围内时,①△PCB的面积大于△QAB的面积?②△PCB的面积小于△QAB的面积?
分析:(1)题目给出了运动时间x分钟,给出了各自的运动速度,可求出线段的大小,然后利用直角三角形的面积公式分别写出函数关系即可;
(2)由(1)知各自的解析式,根据题意面积相等,列出方程,通过解方程可得答案;
(3)根据题目的要求,列出不等式,并通过解不等式得到答案.
(2)由(1)知各自的解析式,根据题意面积相等,列出方程,通过解方程可得答案;
(3)根据题目的要求,列出不等式,并通过解不等式得到答案.
解答:解:(1)依题意得:y1=
PB•CB=
(4-x)•4=8-2x(0≤x≤2)
y2=
BQ•AB=
×4•2x=4x(0<x≤2)
(2)当y1=y2时,8-2x=4x
∴x=
(3)当y1>y2时,8-2x>4x
∴x<
当y1<y2,8-2x<4x
∴x>
答:(1)函数关系式分别为:y1=8-2x(0≤x≤2);y2=4x(0<x≤2);
(2)同时移动
•分钟;这两个三角形面积相等;
(3)移动时间0<x<
时,△PCB的面积大于△QAB的面积;
<x≤2时,△PCB的面积小于△QAB的面积.
| 1 |
| 2 |
| 1 |
| 2 |
y2=
| 1 |
| 2 |
| 1 |
| 2 |
(2)当y1=y2时,8-2x=4x
∴x=
| 4 |
| 3 |
(3)当y1>y2时,8-2x>4x
∴x<
| 4 |
| 3 |
当y1<y2,8-2x<4x
∴x>
| 4 |
| 3 |
答:(1)函数关系式分别为:y1=8-2x(0≤x≤2);y2=4x(0<x≤2);
(2)同时移动
| 4 |
| 3 |
(3)移动时间0<x<
| 4 |
| 3 |
| 4 |
| 3 |
点评:本题考查了一次函数的综合应用;利用函数的关系式依据题目的要求或通过方程或通过不等式求解时解答此类题目的最常用方法,要熟练掌握.

练习册系列答案
相关题目
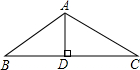 如图所示,在等腰三角形ABC中,AB=AC=12cm,∠ABC=30°,那么底边上的高AD=
如图所示,在等腰三角形ABC中,AB=AC=12cm,∠ABC=30°,那么底边上的高AD= 如图所示,在等腰三角形ABC中,AB=AC=13cm,底边BC=10cm,求底边上的高AD和△ABC的面积.
如图所示,在等腰三角形ABC中,AB=AC=13cm,底边BC=10cm,求底边上的高AD和△ABC的面积.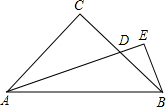 如图所示,在等腰三角形ABC中,∠C=90°,AD是∠BAC的平分线,∠E=90°,那么AD与BE的长度关系为
如图所示,在等腰三角形ABC中,∠C=90°,AD是∠BAC的平分线,∠E=90°,那么AD与BE的长度关系为