题目内容
 如图,直线a、b相交于点A,C、E分别是直线b、a上两点且BC⊥a,DE⊥b,点M、N是中点.
如图,直线a、b相交于点A,C、E分别是直线b、a上两点且BC⊥a,DE⊥b,点M、N是中点.
求证:(1)DM=BM;(2)MN⊥BD.
证明:(1)∵BC⊥a,DE⊥b,
∴∠CDE=∠CBE=90°,
∴△CBE,△CDE为直角三角形,
∵点M是中点,
∴DM=BM= EC,
EC,
∴DM=BM;
(2)∵DM=BM,
∴△MDB为等腰三角形,
又∵N为BD的中点,
∴MN为BD边上的中线,
∴MN⊥BD(三线合一).
分析:(1)由BC⊥a,DE⊥b,易得△CBE,△CDE为直角三角形,又由点M是EC中点,根据直角三角形斜边的中线等于斜边的一半,即可证得:DM=BM;
(2)根据等腰三角形中的三线合一,即可证得.
点评:此题考查了直角三角形中斜边的中线等于斜边的一半与等腰三角形的三线合一的性质.此题图形比较复杂,但难度不大,解题的关键是要注意数形结合思想的应用.
∴∠CDE=∠CBE=90°,
∴△CBE,△CDE为直角三角形,
∵点M是中点,
∴DM=BM=
 EC,
EC,∴DM=BM;
(2)∵DM=BM,
∴△MDB为等腰三角形,
又∵N为BD的中点,
∴MN为BD边上的中线,
∴MN⊥BD(三线合一).
分析:(1)由BC⊥a,DE⊥b,易得△CBE,△CDE为直角三角形,又由点M是EC中点,根据直角三角形斜边的中线等于斜边的一半,即可证得:DM=BM;
(2)根据等腰三角形中的三线合一,即可证得.
点评:此题考查了直角三角形中斜边的中线等于斜边的一半与等腰三角形的三线合一的性质.此题图形比较复杂,但难度不大,解题的关键是要注意数形结合思想的应用.

练习册系列答案
相关题目
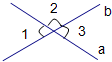 2、如图,直线a、b相交,∠1=36°,则∠3=( )
2、如图,直线a、b相交,∠1=36°,则∠3=( ) 13、如图,直线a、b相交,∠1=65°,则∠2的度数是
13、如图,直线a、b相交,∠1=65°,则∠2的度数是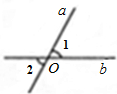 如图,直线a,b相交于点O,若∠1=60°,则∠2=
如图,直线a,b相交于点O,若∠1=60°,则∠2= 如图,直线a,b相交,∠2+∠3=100°,则∠1=
如图,直线a,b相交,∠2+∠3=100°,则∠1=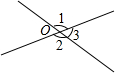 如图,直线m与n相交于点O,若∠1与∠2的和为200°,则∠3为( )
如图,直线m与n相交于点O,若∠1与∠2的和为200°,则∠3为( )