题目内容
矩形ABCD中,AB=3,BC=4,以AB为轴旋转一周得到圆柱,则它的表面积是
- A.60π
- B.56π
- C.32π
- D.24π
B
分析:表面积=侧面积+两个底面积=底面周长×高+2πr2.
解答:∵以直线AB为轴旋转一周得到的圆柱体,得出底面半径为4cm,母线长为3cm,
∴圆柱侧面积=2π•AB•BC=2π•3×4=24π(cm2),
∴底面积=π•BC2=π•42=16π(cm2),
∴圆柱的表面积=24π+2×16π=56π(cm2).
故选B.
点评:此题主要考查了圆柱的表面积的计算公式,根据旋转得到圆柱体,利用圆柱体的侧面积等于底面圆的周长乘以母线长是解决问题的关键.
分析:表面积=侧面积+两个底面积=底面周长×高+2πr2.
解答:∵以直线AB为轴旋转一周得到的圆柱体,得出底面半径为4cm,母线长为3cm,
∴圆柱侧面积=2π•AB•BC=2π•3×4=24π(cm2),
∴底面积=π•BC2=π•42=16π(cm2),
∴圆柱的表面积=24π+2×16π=56π(cm2).
故选B.
点评:此题主要考查了圆柱的表面积的计算公式,根据旋转得到圆柱体,利用圆柱体的侧面积等于底面圆的周长乘以母线长是解决问题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
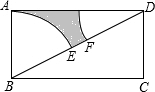 如图,已知矩形ABCD中,AB=8,BC=5π.分别以B,D为圆心,AB为半径画弧,两弧分别交对角线BD于点E,F,则图中阴影部分的面积为( )
如图,已知矩形ABCD中,AB=8,BC=5π.分别以B,D为圆心,AB为半径画弧,两弧分别交对角线BD于点E,F,则图中阴影部分的面积为( )| A、4π | B、5π | C、8π | D、10π |
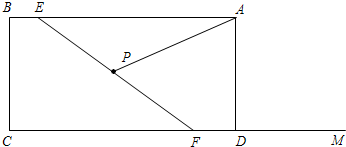
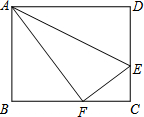 如图,矩形ABCD中,AB=4,AD=5,E是CD上的一点,将△ADE沿AE折叠,点D刚好与BC边上点F重合,则线段CE的长为( )
如图,矩形ABCD中,AB=4,AD=5,E是CD上的一点,将△ADE沿AE折叠,点D刚好与BC边上点F重合,则线段CE的长为( )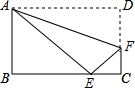 如图,矩形ABCD中,AB=8,BC=10,沿AF折叠矩形ABCD,使点D刚好落在边BC上的点E处,则折痕AF的长为
如图,矩形ABCD中,AB=8,BC=10,沿AF折叠矩形ABCD,使点D刚好落在边BC上的点E处,则折痕AF的长为