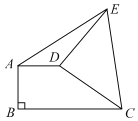
��Ŀ����
����Ŀ��ij�ۺ�ʵ��С���ͬѧ�Ա�У���꼶ѧ�������Ķ���ϲ����ͼ����������˵���.
��1�����ۺ�ʵ��С����������еĵ��鷽ʽ���ȽϺ������� ����д��ż��ɣ�
A�����꼶�������ѧ�δ��������ʾ�����
B�����꼶��1�����ȫ��ͬѧ�����ʾ�����
C�����꼶����ѧ��Ϊ![]() �ı�����ͬѧ�����ʾ�����
�ı�����ͬѧ�����ʾ�����
��2��С��ͬѧ�����ʾ����飨ÿ���������ѧ��ֻ��ѡ������һ��Ľ����������������ͳ��ͼ������������
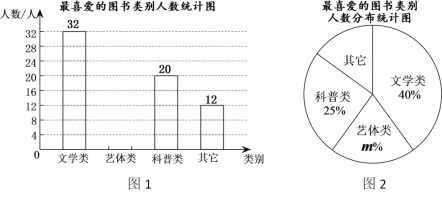
����������Ϣ���ش��������⣺
����α������ѧ������ �ˣ�
���뽫ͼ1������������ͼ�ϱ�����ݣ�
��ͼ2�У�![]() ���������ࡱ�������ε�Բ�Ľ���
���������ࡱ�������ε�Բ�Ľ��� ![]() ��
��
������У���꼶����ѧ��![]() �ˣ����ݵ��������ƴ��꼶��ϲ������ѧ�ࡱͼ���ѧ��Լ�� �ˣ�
�ˣ����ݵ��������ƴ��꼶��ϲ������ѧ�ࡱͼ���ѧ��Լ�� �ˣ�
���𰸡���1��C����2����![]() ���ڼ���������
���ڼ���������![]() ��
��![]() ����
����![]() ��
��
��������
��1�����ݳ�������Ķ������ɵã�
��2�����ȸ�����ѧ�ࣨ������ࣩ��������ٷֱ������������
��������������������ɲ�ȫ����ͳ��ͼ��
�������������������������������m��ֵ����360����������������������ռ�ٷֱȼ��ɵ�Բ�ĽǶ�����
�ܰ��꼶������������ϲ������ѧ����ͼ���ѧ�����ٷֱȼ��ɵý⣮
��1��C���˳�������������������д����ԣ���ѡC��
��2����32��40%=![]() ���ˣ���
���ˣ���
��ϲ��������ͼ�������=80-32-20-12=16
��ȫͳ��ͼ��ͼ��ʾ��
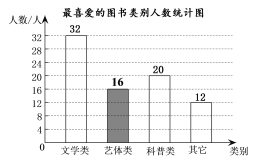
��16��80=20%��
��![]() ��
��
360���25%=90����
�������������������ε�Բ�Ľ���90��.
��320��40%=128���ˣ���
���ԣ����ƴ��꼶��ϲ������ѧ����ͼ���ѧ��Լ��128�ˣ�

����Ŀ���������̨�����ʶ�������Ŀ������ͬѧ�ǵĶ������飬Ϊ������ѧ��������飬����������ijУ���꼶����ѧ���Ŀ����Ķ���������������飬�������������֣�ѧ�������Ķ��ı������ٵ���5����������8���������ݵ����������˲�������ͼ������ͼ��ʾ��
���������� | Ƶ���������� | Ƶ�� |
5 | a | 0.2 |
6 | 18 | 0.36 |
7 | 14 | b |
8 | 8 | 0.16 |
�ϼ� | 50 | c |
���Ƕ���Ƶ��=![]() �������ɱ������ǿ���֪���������������г�������Ϊ50�˿����Ķ���Ϊ6����ͬѧΪ18�ˣ�������������Ӧ��Ƶ�ʾ���
�������ɱ������ǿ���֪���������������г�������Ϊ50�˿����Ķ���Ϊ6����ͬѧΪ18�ˣ�������������Ӧ��Ƶ�ʾ���![]() =0.36��
=0.36��
��1��ͳ�Ʊ��е�a��b��c��ֵ��
��2���뽫Ƶ���ֲ���ֱ��ͼ����������
��3�������б�����ѧ�������Ķ���ƽ��������
��4������У���꼶����600��ѧ��������Ϊ�������ϵ��������Թ��������У���꼶ѧ�������Ķ���Ϊ7����8����������Ϊ��������д����ļ�����̣�