题目内容
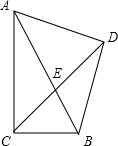 一副直角三角板如图放置(∠ACB=∠ADB=90°),∠CAB=30°,∠BAD=45°,AB交CD于E,则∠CEB的度数是
一副直角三角板如图放置(∠ACB=∠ADB=90°),∠CAB=30°,∠BAD=45°,AB交CD于E,则∠CEB的度数是
- A.30°
- B.45°
- C.60°
- D.75°
D
分析:首先根据∠ACB=∠ADB=90°可判断出A、C、B、D四点共圆,即可由圆周角定理得到∠DAB=∠ABD=∠ACD=45°,进而可在△ACE中,由三角形的外角性质求得∠CEB的度数.
解答:∵∠ADB=90°,∠DAB=45°,
∴△DAB是等腰直角三角形,
∴∠DAB=∠ABD=45°;
由于∠ACB=∠ADB=90°,所以A、C、B、D四点共圆,且直径为AB;
由圆周角定理知:∠ACD=∠ABD=45°;
△ACE中,外角∠CEB=∠CAB+∠ACD=30°+45°=75°;
故选D.
点评:此题主要考查的是圆周角定理和三角形外角性质的综合应用,能够判断出A、C、B、D四点共圆,是解决此题的关键.
分析:首先根据∠ACB=∠ADB=90°可判断出A、C、B、D四点共圆,即可由圆周角定理得到∠DAB=∠ABD=∠ACD=45°,进而可在△ACE中,由三角形的外角性质求得∠CEB的度数.
解答:∵∠ADB=90°,∠DAB=45°,
∴△DAB是等腰直角三角形,
∴∠DAB=∠ABD=45°;
由于∠ACB=∠ADB=90°,所以A、C、B、D四点共圆,且直径为AB;
由圆周角定理知:∠ACD=∠ABD=45°;
△ACE中,外角∠CEB=∠CAB+∠ACD=30°+45°=75°;
故选D.
点评:此题主要考查的是圆周角定理和三角形外角性质的综合应用,能够判断出A、C、B、D四点共圆,是解决此题的关键.

练习册系列答案
相关题目
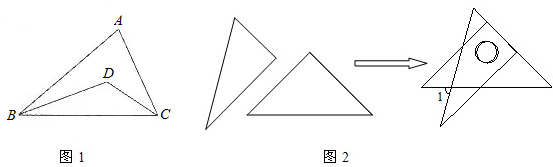
 12、将一副直角三角板如图放置,使含30°角的三角板的段直角边和含45°角的三角板的一条直角边重合,则∠1的度数为
12、将一副直角三角板如图放置,使含30°角的三角板的段直角边和含45°角的三角板的一条直角边重合,则∠1的度数为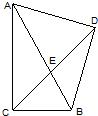 7、一副直角三角板如图放置(∠ACB=∠ADB=90°),∠CAB=30°,∠BAD=45°,AB交CD于E,则∠CEB的度数是( )
7、一副直角三角板如图放置(∠ACB=∠ADB=90°),∠CAB=30°,∠BAD=45°,AB交CD于E,则∠CEB的度数是( ) (2012•海门市模拟)一副直角三角板如图放置,点A在DF的延长线上,BC∥DA,∠D=∠BAC=90°,∠C=45°,∠E=30°,AC=10.
(2012•海门市模拟)一副直角三角板如图放置,点A在DF的延长线上,BC∥DA,∠D=∠BAC=90°,∠C=45°,∠E=30°,AC=10.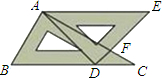 将一副直角三角板如图放置,己知∠AFD=75°,AE和BC平行吗?请说明理由.
将一副直角三角板如图放置,己知∠AFD=75°,AE和BC平行吗?请说明理由.