题目内容
4个三角形的边长分别为:
①a=5,b=12,c=13;
②a=2,b=3,c=4;
③a=2.5,b=6,c=6.5;
④a=21,b=20,c=29.
其中,直角三角形的个数是________(填序号).
3
分析:分别求出a2+b2和c2的值,看看a2+b2和c2是否相等即可.
解答:①∵a2+b2=52+122=169,c2=132=169,
∴a2+b2=c2,
∴三角形是直角三角形,∴①正确;
②∵a2+b2=22+32=13,c2=42=16,
∴a2+b2≠c2,
∴三角形不是直角三角形,∴②错误;
③∵a2+b2=2.52+62=42.25,c2=6.52=42.25,
∴a2+b2=c2,
∴三角形是直角三角形,∴③正确;
④∵a2+b2=212+202=841,c2=292=841,
∴a2+b2=c2,
∴三角形是直角三角形,∴④正确;
即正确的有3个,
故答案为:3.
点评:本题考查了勾股定理的逆定理的应用,注意:如果一个三角形的两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
分析:分别求出a2+b2和c2的值,看看a2+b2和c2是否相等即可.
解答:①∵a2+b2=52+122=169,c2=132=169,
∴a2+b2=c2,
∴三角形是直角三角形,∴①正确;
②∵a2+b2=22+32=13,c2=42=16,
∴a2+b2≠c2,
∴三角形不是直角三角形,∴②错误;
③∵a2+b2=2.52+62=42.25,c2=6.52=42.25,
∴a2+b2=c2,
∴三角形是直角三角形,∴③正确;
④∵a2+b2=212+202=841,c2=292=841,
∴a2+b2=c2,
∴三角形是直角三角形,∴④正确;
即正确的有3个,
故答案为:3.
点评:本题考查了勾股定理的逆定理的应用,注意:如果一个三角形的两边的平方和等于第三边的平方,那么这个三角形是直角三角形.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
 ,c=6;②a=2,b=3,c=
,c=6;②a=2,b=3,c=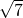 ;③a=2.5,b=6,c=6.5;④a=10.5,b=10,c=14.5.
;③a=2.5,b=6,c=6.5;④a=10.5,b=10,c=14.5.