题目内容
如图，已知直线y=-
x+1交坐标轴于A、B两点，以线段AB为边向上作正方形ABCD，过A、D、C作抛物线L1．
（1）请直接写出点C、D的坐标；
（2）求抛物线L1的解析式；
（3）若正方形以每秒
个长度单位的速度沿射线AB下滑，直至顶点D落在x轴上时停止．设正方形在运动过程中落在x轴下方部分的面积为S．求S关于滑行时间t的函数关系式；
（4）在（3）的条件下，抛物线L1与正方形一起平移，同时停止，得到抛物线L2．两抛物线的顶点分别为M、N，点 P是x轴上一动点，点Q是抛物线L1上一动点，是否存在这样的点P、Q，使得以M、N、P、Q为顶点的四边形为平行四边形？若存在，直接写出点P的坐标；若不存在，请说明理由．
| 1 |
| 2 |
（1）请直接写出点C、D的坐标；
（2）求抛物线L1的解析式；
（3）若正方形以每秒
| 5 |
（4）在（3）的条件下，抛物线L1与正方形一起平移，同时停止，得到抛物线L2．两抛物线的顶点分别为M、N，点 P是x轴上一动点，点Q是抛物线L1上一动点，是否存在这样的点P、Q，使得以M、N、P、Q为顶点的四边形为平行四边形？若存在，直接写出点P的坐标；若不存在，请说明理由．
分析：（1）首先由直线AB的解析式求出A、B两点的坐标，过D作DE⊥y轴于E，通过构建的全等三角形：△ADE和△BAO，可以求出DE、AE的长，进而能得到点D的坐标；C点坐标的求法同理．
（2）利用待定系数法求抛物线的解析式即可．
（3）随着正方形的移动，正方形在x轴下方的形状会不断的变化，所以要注意三个关键点：A、C、D三点运动到x轴上时t的值，若是这三个值分别是α、β、γ，那么分三种情况：
①0＜t≤α时，正方形在x轴下方的是个小直角三角形；
②α＜t≤β时，正方形在x轴下方的是个梯形；
③β＜t≤γ时，正方形在x轴下方的是个五边形，其面积可由正方形的面积减去x轴上方的小直角三角形得出．
（4）由前面两小题可知道M、D两点的坐标；由相似三角形：△ABO和△HBE可以求出点H的坐标，由于抛物线L1沿直线AB移动，所以M→N与D→H的移动规律是相同的，可据此得出点N的坐标；由于点P在x轴上，所以MN只可能是平行四边形的边（若MN是对角线，那么点Q必在直线MN的上方，显然不合题意），那么点Q的纵坐标可由M、N的纵坐标差的绝对值得出，在确定点Q的坐标后，根据M→N的平移规律即可得出点P的坐标．
（2）利用待定系数法求抛物线的解析式即可．
（3）随着正方形的移动，正方形在x轴下方的形状会不断的变化，所以要注意三个关键点：A、C、D三点运动到x轴上时t的值，若是这三个值分别是α、β、γ，那么分三种情况：
①0＜t≤α时，正方形在x轴下方的是个小直角三角形；
②α＜t≤β时，正方形在x轴下方的是个梯形；
③β＜t≤γ时，正方形在x轴下方的是个五边形，其面积可由正方形的面积减去x轴上方的小直角三角形得出．
（4）由前面两小题可知道M、D两点的坐标；由相似三角形：△ABO和△HBE可以求出点H的坐标，由于抛物线L1沿直线AB移动，所以M→N与D→H的移动规律是相同的，可据此得出点N的坐标；由于点P在x轴上，所以MN只可能是平行四边形的边（若MN是对角线，那么点Q必在直线MN的上方，显然不合题意），那么点Q的纵坐标可由M、N的纵坐标差的绝对值得出，在确定点Q的坐标后，根据M→N的平移规律即可得出点P的坐标．
解答：
解：（1）由直线y=-
x+1知：A（0，1）、B（2，0）；
过D作DE⊥y轴于E；
在△ADE与△BAO中，
∴△ADE≌△BAO（AAS），
则：AE=OB=2，DE=OA=1；
∴OE=OA+AE=3，则：D（1，3）；
由于CD、AB是正方形的一组对边，所以AB
CD；
∵点A向下平移1个单位，再向右平移2个单位得B点，
∴点D向下平移1个单位，再向右平移2个单位得C点，即：C（3，2）；
综上，C（3，2）、D（1，3）．
（2）易知A（0，1），设抛物线L1的解析式为y=ax2+bx+c（a≠0），则有：
，
解得
则：y=-
x2+
x+1．
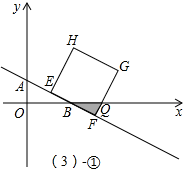
（3）①当0＜t≤1时，如图①
Rt△AOB中，tan∠ABO=
=
，
Rt△QFB中，tan∠QBF=tan∠ABO=
，BF=
t，
∴QF=tan∠QBF•BF=
；
则：S=
BF•QF=
•
t•
=
；
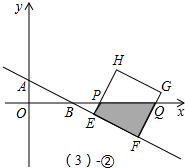
②当1＜t≤2时，如图②，BF=
t，BE=
t-
；
∴PE=tan∠QBF•BE=
，QF=
；
则：S=
（PE+QF）•EF=
（t-1+t）•
=
t-
；
③当2＜t≤3时，如图③，
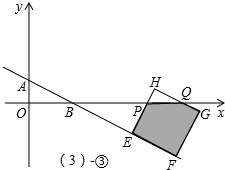Rt△HQP中，tan∠HQP=tan∠QBF=
，
HP=HE-PE=
-
=
；
∴HQ=
=2HP=3
-
t；
则：S=S正方形EFGH-S△HPQ=（
）2-
=-
t2+
t-
．
（4）∵∠ABO=∠HBE，∠AOB=∠HEB=90°，
∴△ABO∽△HBE，
得：
=
，即：
=
，
解得：BH=5；
∴H（7，0）；
由D（1，3）、H（7，0）知，M向右平移6个单位，向下平移3个单位即可得到N点；
因为点P在x轴上，若以M、N、P、Q为顶点的四边形为平行四边形（MN只能是平行四边形的边），则点Q的纵坐标必为±3；
当点Q的纵坐标为3时，代入抛物线的解析式可得：Q（1，3）或（
，3），向右平移6个单位，向下平移3个单位得：P（7，0）或（
，0）；
当点Q的纵坐标为-3时，代入抛物线的解析式可得：Q（
，-3），向左平移6个单位，向上平移3个单位得：P（
，0）或（
，0）；
综上，存在符合条件的P点，其坐标为（7，0）或（
，0）或（
，0）或（
，0）．
解：（1）由直线y=-| 1 |
| 2 |
过D作DE⊥y轴于E；
在△ADE与△BAO中，
|
∴△ADE≌△BAO（AAS），
则：AE=OB=2，DE=OA=1；
∴OE=OA+AE=3，则：D（1，3）；
由于CD、AB是正方形的一组对边，所以AB
| ∥ |
. |
∵点A向下平移1个单位，再向右平移2个单位得B点，
∴点D向下平移1个单位，再向右平移2个单位得C点，即：C（3，2）；
综上，C（3，2）、D（1，3）．
（2）易知A（0，1），设抛物线L1的解析式为y=ax2+bx+c（a≠0），则有：
|
解得
|
则：y=-
| 5 |
| 6 |
| 17 |
| 6 |
（3）①当0＜t≤1时，如图①
Rt△AOB中，tan∠ABO=
| OA |
| OB |
| 1 |
| 2 |
Rt△QFB中，tan∠QBF=tan∠ABO=
| 1 |
| 2 |
| 5 |
∴QF=tan∠QBF•BF=
| ||
| 2 |
则：S=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| ||
| 2 |
| 5t2 |
| 4 |
②当1＜t≤2时，如图②，BF=
| 5 |
| 5 |
| 5 |
∴PE=tan∠QBF•BE=
| ||||
| 2 |
| ||
| 2 |
则：S=
| 1 |
| 2 |
| ||
| 4 |
| 5 |
| 5 |
| 2 |
| 5 |
| 4 |
③当2＜t≤3时，如图③，
Rt△HQP中，tan∠HQP=tan∠QBF=| 1 |
| 2 |
HP=HE-PE=
| 5 |
| ||||
| 2 |
3
| ||||
| 2 |
∴HQ=
| HP |
| tan∠HQP |
| 5 |
| 5 |
则：S=S正方形EFGH-S△HPQ=（
| 5 |
(3
| ||||
| 4 |
| 5 |
| 4 |
| 15 |
| 2 |
| 25 |
| 4 |
（4）∵∠ABO=∠HBE，∠AOB=∠HEB=90°，
∴△ABO∽△HBE，
得：
| AB |
| BH |
| OA |
| HE |
| ||
| BH |
| 1 | ||
|
解得：BH=5；
∴H（7，0）；
由D（1，3）、H（7，0）知，M向右平移6个单位，向下平移3个单位即可得到N点；
因为点P在x轴上，若以M、N、P、Q为顶点的四边形为平行四边形（MN只能是平行四边形的边），则点Q的纵坐标必为±3；
当点Q的纵坐标为3时，代入抛物线的解析式可得：Q（1，3）或（
| 12 |
| 5 |
| 42 |
| 5 |
当点Q的纵坐标为-3时，代入抛物线的解析式可得：Q（
17±
| ||
| 10 |
-43-
| ||
| 10 |
-43+
| ||
| 10 |
综上，存在符合条件的P点，其坐标为（7，0）或（
| 42 |
| 5 |
-43-
| ||
| 10 |
-43+
| ||
| 10 |
点评：此题主要考查了二次函数解析式的确定、图形面积的求法、相似三角形和全等三角形的应用、图形的平移及其性质、平行四边形的性质等综合知识；（3）题中，一定要抓住图形平移过程中的关键点，在对自变量的取值范围进行界定时，一定要做到不重不漏；最后一题中，首先要判断出MN是平行四边形的边或对角线，然后根据点M、N的坐标来确定P、Q的位置关系；总体来看，题目的难度较大．
练习册系列答案
阅读快车系列答案
相关题目
16、如图，已知直线AB和CD相交于点O，∠COE是直角，OF平分∠AOE．
5、如图，已知直线l1∥l2，AB⊥CD，∠1=30°，则∠2的度数为（ ）
如图，已知直线l1：
（2013•怀化）如图，已知直线a∥b，∠1=35°，则∠2=
如图，已知直线m∥n，则下列结论成立的是（ ）