题目内容
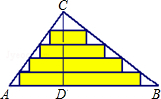（2013•江阴市一模）如图，△ABC是一张直角三角形彩色纸，AC=30cm，BC=40cm．若将斜边上的高CD n等分，然后裁出（n-1）张宽度相等的长方形纸条．则这（n-1）张纸条的面积和是| 600(n-1) |
| n |
| 600(n-1) |
| n |
分析：由△ABC是一张直角三角形彩色纸，AC=30cm，BC=40cm由勾股定理即可求得AB的长，然后利用三角形的面积，求得高CD的长，继而可求得纸条宽度，然后利用相似三角形的对应边成比例，即可求得EF，GH以及KL的长，继而求得这（n-1）张纸条的面积和．
解答：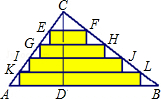
解：∵△ABC是直角三角形，AC=30cm，BC=40cm．
∴AB=
=50（cm），
∵S△ABC=
AC•BC=
AB•CD，
∴AC•BC=AB•CD，
∴30×40=50•CD，
∴CD=24cm．
可知纸条宽度为：
cm，
∵EF∥AB，
∴△CEF∽△CAB，
∴
=
，
∴EF=
AB，
同理：GH=
AB，KL=
AB，
∴（n-1）张纸条的面积和为：
（EF+GH+…+KL）•
=（
+
+…+
）×50×
=
[1+2+…+（n-1）]×50×
=
（cm2）．
故答案为：
．
解：∵△ABC是直角三角形，AC=30cm，BC=40cm．∴AB=
| 302+402 |
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴AC•BC=AB•CD，
∴30×40=50•CD，
∴CD=24cm．
可知纸条宽度为：
| 24 |
| n |
∵EF∥AB，
∴△CEF∽△CAB，
∴
| EF |
| AB |
| 1 |
| n |
∴EF=
| 1 |
| n |
同理：GH=
| 2 |
| n |
| n-1 |
| n |
∴（n-1）张纸条的面积和为：
（EF+GH+…+KL）•
| 24 |
| n |
=（
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| 24 |
| n |
=
| 1 |
| n |
| 24 |
| n |
=
| 600(n-1) |
| n |
故答案为：
| 600(n-1) |
| n |
点评：此题考查了相似三角形的判定与性质与勾股定理的应用．此题难度适中，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
