题目内容
在一个四边形ABCD中，依次连接各边中点所得到的四边形是（ ）
| A、平行四边形 | B、菱形 | C、矩形 | D、正方形 |
分析：三角形的中位线平行于第三边，且等于第三边的一半．需注意新四边形的形状只与对角线有关，不用考虑原四边形的形状．
解答：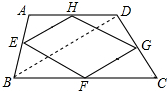
解：连接BD，
∵四边形ABCD，E、F、G、H分别是各边中点，
∴在△ABD中，E、H是AB、AD中点，
∴EH∥BD，EH=
BD，
在△BCD中，G、F是DC、BC中点，
∴GF∥BD，GF=
BD，
∴EH=GF，EH∥DF，
∴四边形EFGH为平行四边形．
故选A．
解：连接BD，∵四边形ABCD，E、F、G、H分别是各边中点，
∴在△ABD中，E、H是AB、AD中点，
∴EH∥BD，EH=
| 1 |
| 2 |
在△BCD中，G、F是DC、BC中点，
∴GF∥BD，GF=
| 1 |
| 2 |
∴EH=GF，EH∥DF，
∴四边形EFGH为平行四边形．
故选A．
点评：本题用三角形的中位线的性质考查了平行四边形的判定：三角形的中位线平行于第三边，且等于第三边的一半．
练习册系列答案
相关题目
在一个四边形ABCD中，依次连接各边中点的四边形是菱形，则对角线AC与BD需要满足条件（ ）
| A、垂直 | B、相等 | C、相交 | D、不再需要条件 |
在一个四边形ABCD中，依次连接各边的中点得一菱形，则对角线AC与BD必须满足（ ）
| A、垂直 | B、相等 | C、互相平分 | D、互相垂直平分 |