题目内容
如图,已知圆锥的高AO为8cm,底面圆的直径BC长为12cm,则此圆锥的侧面展开图的圆心角为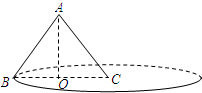
分析:根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得求解.
解答:解:根据勾股定理可知母线长为
=10cm,
则根据侧面展开图扇形的弧长等于圆锥底面周长可得:
12π=
,
n=216°.
| 64+36 |
则根据侧面展开图扇形的弧长等于圆锥底面周长可得:
12π=
| nπ•10 |
| 180 |
n=216°.
点评:主要考查了圆锥侧面展开扇形与底面圆之间的关系,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把的扇形的弧长等于圆锥底面周长作为相等关系,列方程求解.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
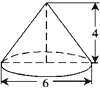 如图,已知圆锥的高为4,底面圆的直径为6,则此圆锥的侧面积是( )
如图,已知圆锥的高为4,底面圆的直径为6,则此圆锥的侧面积是( )| A、12π | B、15π | C、24π | D、30π |
 9、如图,已知圆锥的高为8,底面圆的直径为12,则此圆锥的侧面积是( )
9、如图,已知圆锥的高为8,底面圆的直径为12,则此圆锥的侧面积是( )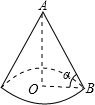 如图,已知圆锥的高AO等于圆锥的底面半径OB的
如图,已知圆锥的高AO等于圆锥的底面半径OB的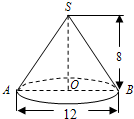 16、如图,已知圆锥的高SO为8cm,底面圆的直径AB为12cm,求此圆锥的侧面积(结果保留π)
16、如图,已知圆锥的高SO为8cm,底面圆的直径AB为12cm,求此圆锥的侧面积(结果保留π)