题目内容
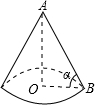如图，已知圆锥的高AO等于圆锥的底面半径OB的| 3 |
分析：圆锥的母线，底面半径，高线正好构成直角三角形，根据三角函数就可以求解．
解答：解：设圆锥的底面半径OB为x，则圆锥的高AO等于
x．
∴tanα=
=
，
又∵tan60°=
，
∴∠α=60°．
| 3 |
∴tanα=
| AO |
| OB |
| 3 |
又∵tan60°=
| 3 |
∴∠α=60°．
点评：此题比较简单，解答此题关键是熟知特殊角的三角函数值．
练习册系列答案
相关题目
9、如图，已知圆锥的高为8，底面圆的直径为12，则此圆锥的侧面积是（ ）
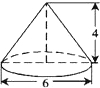如图，已知圆锥的高为4，底面圆的直径为6，则此圆锥的侧面积是（ ）| A、12π | B、15π | C、24π | D、30π |
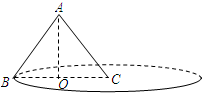
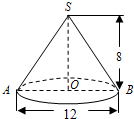16、如图，已知圆锥的高SO为8cm，底面圆的直径AB为12cm，求此圆锥的侧面积（结果保留π）