题目内容
 如图,函数
如图,函数 在第一象限的图象上有一点C(1,5),过点C的直线y=-kx+b(k>0)与x轴交于点A(a,0).
在第一象限的图象上有一点C(1,5),过点C的直线y=-kx+b(k>0)与x轴交于点A(a,0).
(1)写出a关于k的函数关系式;
(2)当该直线与双曲线 在第一象限的另一交点D的横坐标是9时,求△COA的面积.
在第一象限的另一交点D的横坐标是9时,求△COA的面积.
解:(1)把C(1,5)代入直线y=-kx+b(k>0)得:-k+b=5,则b=5+k;
把(a,0)代入直线y=-kx+b(k>0)得:-ak+b=0,
把b=5+k代入-ak+b=0,得:-ak+5+k=0,解得:a= ;
;
(2)把x=9代入y= 得:y=
得:y= ,则D的坐标是(9,
,则D的坐标是(9, ),
),
直线AC的解析式是y=-kx+b,把C、D两点代入得,
根据题意得: ,
,
解得: ,
,
则AC的解析式是:y=- x+
x+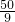 .
.
令y=0,解得:x=10.
则OA=10,
则△COA的面积= ×10×5=25.
×10×5=25.
分析:(1)把C和A的坐标代入直线的解析式,然后消去b即可得到a关于k的函数关系式;
(2)首先求得D的坐标,然后利用待定系数法即可求得AC的解析式,则A的坐标即可求得,即OA的长度可以求得,然后利用三角形的面积公式求解.
点评:.本题是一次函数与反比例函数的综合题,考查了待定系数法求函数的解析式,正确求得AC的解析式是关键.
把(a,0)代入直线y=-kx+b(k>0)得:-ak+b=0,
把b=5+k代入-ak+b=0,得:-ak+5+k=0,解得:a=
 ;
;(2)把x=9代入y=
 得:y=
得:y= ,则D的坐标是(9,
,则D的坐标是(9, ),
),直线AC的解析式是y=-kx+b,把C、D两点代入得,
根据题意得:
 ,
,解得:
 ,
,则AC的解析式是:y=-
 x+
x+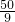 .
.令y=0,解得:x=10.
则OA=10,
则△COA的面积=
 ×10×5=25.
×10×5=25.分析:(1)把C和A的坐标代入直线的解析式,然后消去b即可得到a关于k的函数关系式;
(2)首先求得D的坐标,然后利用待定系数法即可求得AC的解析式,则A的坐标即可求得,即OA的长度可以求得,然后利用三角形的面积公式求解.
点评:.本题是一次函数与反比例函数的综合题,考查了待定系数法求函数的解析式,正确求得AC的解析式是关键.

练习册系列答案
相关题目
 ,
, ,
, 在反比例函数
在反比例函数 的图象上,则下列结论正确的是
的图象上,则下列结论正确的是



 的图象在第( )象限
的图象在第( )象限 图象上一点,则此函数图象必经过点
图象上一点,则此函数图象必经过点 在第一象限内的图象,它关于y轴对称的图象对应的函数关系式是
在第一象限内的图象,它关于y轴对称的图象对应的函数关系式是
 (x<0)
(x<0) (x<0)
(x<0) (x>0)
(x>0) ,
, ,
, 在反比例函数
在反比例函数 的图象上,则下列结论正确的是
的图象上,则下列结论正确的是



 的图象在第( )象限
的图象在第( )象限 图象上一点,则此函数图象必经过点
图象上一点,则此函数图象必经过点 在第一象限内的图象,它关于y轴对称的图象对应的函数关系式是
在第一象限内的图象,它关于y轴对称的图象对应的函数关系式是
 (x<0)
(x<0) (x<0)
(x<0) (x>0)
(x>0)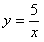 在第一象限的图象上有一点C(1,5),过点C的直线y=-kx+b(k>0)与x轴交于点A(a,0)。
在第一象限的图象上有一点C(1,5),过点C的直线y=-kx+b(k>0)与x轴交于点A(a,0)。
 在第一象限的另一交点D的横坐标是9时,求△COA的面积。
在第一象限的另一交点D的横坐标是9时,求△COA的面积。 在第一象限的图象上有一点C(1,5),过点C的直线y=-kx+b(k>0)与x轴交于点A(a,0).
在第一象限的图象上有一点C(1,5),过点C的直线y=-kx+b(k>0)与x轴交于点A(a,0). 在第一象限的另一交点D的横坐标是9时,求△COA的面积.
在第一象限的另一交点D的横坐标是9时,求△COA的面积.