题目内容
我们在学习实数时，画了这样一个图：即以数轴上1个单位长的线段为边作正方形，再以原点O为圆心，正方形的对角线OB长为半径作弧，交x轴于点A．请根据图形填空．
（1）线段OA=______个单位长；
（2）这个图形的目的是为了说明______；
（3）这种研究和解决问题的方式，体现的数学思想方法是______．
解：（1）根据题意知，OA=OB．
OB2=12+12=2，
∴OB=
，
∴OA=．
（2）这个图形的目的是为了说明数轴上的点和实数-一对应关系；
（3）此题借助于实数与数轴的关键求得线段OA的长度，体现了数形结合的数学思想．
故答案是：；数轴上的点和实数-一对应关系；数形结合．
分析：（1）根据题意知，OA=OB，所以在正方形中利用勾股定理求得对角线OB的长度即可；
（2）根据数轴上的点与实数的对应关系即可求解；
（3）根据所学的数学思想方法并结合题意即可求解．
点评：本题主要考查了实数与数轴之间的定义关系，此题综合性较强，不仅要结合图形，还需要熟悉平方根的定义．也要求学生了解数形结合的数学思想．
OB2=12+12=2，
∴OB=
，∴OA=
．（2）这个图形的目的是为了说明数轴上的点和实数-一对应关系；
（3）此题借助于实数与数轴的关键求得线段OA的长度，体现了数形结合的数学思想．
故答案是：
；数轴上的点和实数-一对应关系；数形结合．分析：（1）根据题意知，OA=OB，所以在正方形中利用勾股定理求得对角线OB的长度即可；
（2）根据数轴上的点与实数的对应关系即可求解；
（3）根据所学的数学思想方法并结合题意即可求解．
点评：本题主要考查了实数与数轴之间的定义关系，此题综合性较强，不仅要结合图形，还需要熟悉平方根的定义．也要求学生了解数形结合的数学思想．
练习册系列答案
相关题目
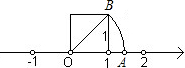我们在学习“实数”时，画了这样一个图，即“以数轴上的单位长为‘1’的线段作一个正方形，然后以原点O为圆心，正方形的对角线长为半径画弧交x轴于点A”，请根据图形回答下列问题：
我们在学习“实数”时，画了这样一个图，即“以数轴上的单位长为1的线段作一个正方形，然后以原点O为圆心，正方形的对角线长为半径画弧交x轴于点A”，则线段OA的长度是
（1）若a、b为实数，且
