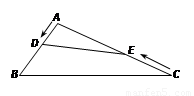题目内容
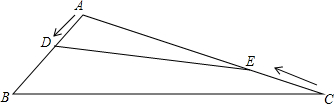
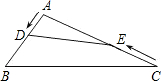 如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm/秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )
如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm/秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )| A、3秒或4.8秒 | B、3秒 | C、4.5秒 | D、4.5秒或4.8秒 |
分析:根据相似三角形的性质,由题意可知有两种相似形式,△ADE∽△ABC和△ADE∽△ACB,可求运动的时间是3秒或4.8秒.
解答:解:根据题意得:设当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是x秒,
①若△ADE∽△ABC,则
=
,
∴
=
,
解得:x=3;
②若△ADE∽△ACB,则
=
,
∴
=
,
解得:x=4.8.
∴当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是3秒或4.8秒.
故选A.
①若△ADE∽△ABC,则
| AD |
| AB |
| AE |
| AC |
∴
| x |
| 6 |
| 12-2x |
| 12 |
解得:x=3;
②若△ADE∽△ACB,则
| AD |
| AC |
| AE |
| AB |
∴
| x |
| 12 |
| 12-2x |
| 6 |
解得:x=4.8.
∴当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是3秒或4.8秒.
故选A.
点评:此题考查了相似三角形的性质,解题时要注意此题有两种相似形式,别漏解;还要注意运用方程思想解题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 14、如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm/秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是
14、如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm/秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是