题目内容
（2012•拱墅区一模）若关于x的方程
+
=2的解为x=4，则m=
| x |
| x-3 |
| 2 |
| m-x |
3
3
．分析：方程两边都乘以最简公分母（x-3）（m-x）把分式方程化为整式方程，再根据方程解的定义，把x=4代入整式方程，解关于m的方程即可．
解答：解：方程两边都乘以（x-3）（m-x）得，
x（m-x）+2（x-3）=2（x-3）（m-x），
∵方程的解是x=4，
∴4（m-4）+2（4-3）=2（4-3）（m-4），
整理得，m-4=-1，
解得m=3．
经检验，当m=3时，方程的解为x=4．
故答案为：3．
x（m-x）+2（x-3）=2（x-3）（m-x），
∵方程的解是x=4，
∴4（m-4）+2（4-3）=2（4-3）（m-4），
整理得，m-4=-1，
解得m=3．
经检验，当m=3时，方程的解为x=4．
故答案为：3．
点评：本题考查了分式方程的解，根据方程解的定义，把方程的解代入进行计算即可，注意对求出的m的值进行检验．
练习册系列答案
阅读快车系列答案
相关题目
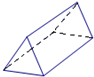（2012•拱墅区一模）下面的展开图能拼成如图立体图形的是（ ）