Question

【题目】综合探究题

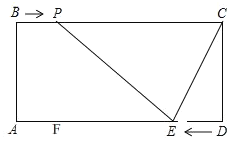
在之前的学习中，我们已经初步了解到，长方形的对边平行且相等，每个角都是.如图，长方形中，，，为边上一动点，从点出发，以向终点运动，同时动点从点出发，以向终点运动，运动的时间为.

（1）当时，①则线段的长=______；

②当平分时，求的值；

（2）若，且是以为腰的等腰三角形，求的值；

（3）连接，直接写出点与点关于对称时与的值.

Answer 1

【答案】(1)①5cm ② (2)3或 (3),t=4

【解析】

(1)①先得出，，，在中，根据勾股定理得，；②当EP平分时，根据角平分线的性质可得：点P到EC的距离等于点P到AD距离，求出BC上的高等于4，根据面积可以求出a的值;
(2)先得出，，，再分两种情况①，②，建立方程即可得出结论；
(3)先判断出，，进而求出，再构造出直角三角形，得出，进而建立方程即可得出结论．

解：(1)① 四边形是长方形，

当时，由运动知，，
,

在中，根据勾股定理得，；
②当EP平分时，根据角平分线的性质可得：

点P到EC的距离等于点P到AD距离，

即：,

,则

.

故.

(2)当时，由运动知，，
，
在中，，
是以CE为腰的等腰三角形，
①，
，
.
②，

，

即：t的值为3或；

(3)如图，

由运动知，，

点C与点E关于对称，
,

过点P作于F，

四边形是长方形，
，
在中，

根据勾股定理得，，
，
.