题目内容
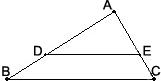7、如图，DE∥BC，且AD：DB=2：1，则DE：BC=2：3
，△ADE与△ABC的面积之比为4：9
．分析：由DE∥BC，易证得△ADE∽△ABC，根据相似三角形的对应线段成比例即可求得DE、BC的比例关系；由相似三角形的面积比等于相似比的平方即可求得两个三角形的面积比．
解答：解：∵AD：DB=2：1，
∴AD：AB=2：3；
∵DE∥BC，
∴△ADE∽△ABC；
∴DE：BC=AD：AB=2：3；
S△ADE：S△ABC=AD2：DB2=4：9．
∴AD：AB=2：3；
∵DE∥BC，
∴△ADE∽△ABC；
∴DE：BC=AD：AB=2：3；
S△ADE：S△ABC=AD2：DB2=4：9．
点评：此题主要考查的是相似三角形的性质：相似三角形的对应线段成比例，面积比等于相似比的平方．
练习册系列答案
阅读快车系列答案
相关题目
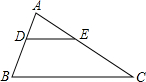如图，DE∥BC，且DB=AE，若AB=5，AC=10，则AE的长为
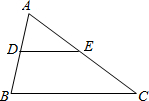如图，DE∥BC，且AD=3，AB=5，CE=3，求AC的长．
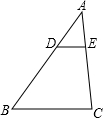如图，DE∥BC，且
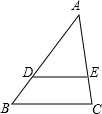如图，DE∥BC，且AD：BD=3：1，则S△ADE：S梯形BCED=（ ）