题目内容
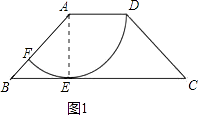
【题目】如图，在四边形ABCD中，AD∥BC，AD=2，AB=2 
，以点A为圆心，AD为半径的圆与BC相切于点E，交AB于点F 
（1）求∠ABE的大小及 
的长度；
（2）在BE的延长线上取一点G，使得 
上的一个动点P到点G的最短距离为2 ﹣2，求BG的长．
【答案】
（1）解：连接AE，如图1，
∵AD为半径的圆与BC相切于点E，
∴AE⊥BC，AE=AD=2．
在Rt△AEB中，
sin∠ABE= 
= 
= 
，
∴∠ABE=45°．
∵AD∥BC，
∴∠DAB+∠ABE=180°，
∴∠DAB=135°，
∴ 
的长度为 
= 
；
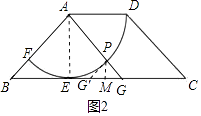
（2）解：如图2，
根据两点之间线段最短可得：
当A、P、G三点共线时PG最短，
此时AG=AP+PG=2+2 
﹣2=2 ，
∴AG=AB．
∵AE⊥BG，
∴BE=EG．
∵BE= 
= 
=2，
∴EG=2，
∴BG=4．
过P作PM垂直BC于M，将PG沿PM翻折得G'，此时BG'=4﹣2×（2﹣√2）=2 ，点G′也满足条件．
综上，存在满足条件的BG=4或2 ．
【解析】（1）连接AE，如图1，根据圆的切线的性质可得AE⊥BC，解Rt△AEB可求出∠ABE，进而得到∠DAB，然后运用圆弧长公式就可求出 的长度；（2）如图2，根据两点之间线段最短可得：当A、P、G三点共线时PG最短，此时AG=AP+PG=2 =AB，根据等腰三角形的性质可得BE=EG，只需运用勾股定理求出BE，就可求出BG的长，再根据对称性求出G′．
【考点精析】通过灵活运用切线的性质定理和弧长计算公式，掌握切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径；若设⊙O半径为R，n°的圆心角所对的弧长为l，则l=nπr/180;注意：在应用弧长公式进行计算时，要注意公式中n的意义．n表示1°圆心角的倍数，它是不带单位的即可以解答此题．
