题目内容
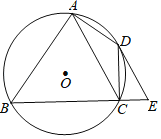
【题目】点A、C为半径是8的圆周上两动点,点B为![]() 的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆半径的中点上,则该菱形的边长为_____.
的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆半径的中点上,则该菱形的边长为_____.
【答案】![]() 或
或![]()
【解析】
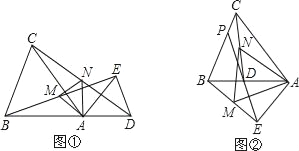
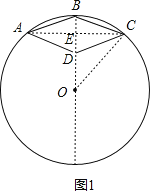
过B作直径,连接AC交BO于E,如图①,根据已知条件得到BD=![]() OB=4,求得OD、OE、DE的长,连接OC,根据勾股定理得到结论;如图②,BD=12,求得OD、OE、DE的长,连接OD,根据勾股定理得到结论.
OB=4,求得OD、OE、DE的长,连接OC,根据勾股定理得到结论;如图②,BD=12,求得OD、OE、DE的长,连接OD,根据勾股定理得到结论.
过B作直径,连接AC交BO于E,
∵点B为![]() 的中点,
的中点,
∴BD⊥AC,
如图①,
∵点D恰在该圆直径上,D为OB的中点,
∴BD=![]() ×8=4,
×8=4,
∴OD=OB-BD=4,
∵四边形ABCD是菱形,
∴DE=![]() BD=2,
BD=2,
∴OE=2+4=6,
连接OC,
∵CE=![]() ,
,
在Rt△DEC中,由勾股定理得:DC=![]() ;
;
如图②,
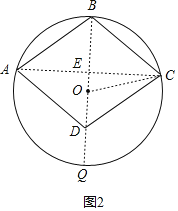
OD=4,BD=8+4=12,DE=![]() BD=6,OE=6-4=2,
BD=6,OE=6-4=2,
由勾股定理得:CE=![]() ,
,
DC=![]() ,
,
故答案为:![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】已知y是x的函数,自变量x的取值范围是x≠0的全体实数,如表是y与x的几组对应值.
x | … | ﹣3 | ﹣2 | ﹣1 | ﹣ | ﹣ |
|
| 1 | 2 | 3 | … |
y | … |
|
| ﹣ | ﹣ | ﹣ |
|
|
| m |
| … |
小华根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
(1)从表格中读出,当自变量是﹣2时,函数值是 ;
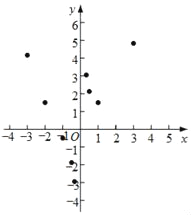
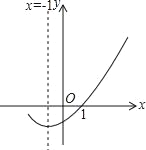
(2)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(3)在画出的函数图象上标出x=2时所对应的点,并写出m= .
(4)结合函数的图象,写出该函数的一条性质: .