Question

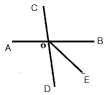
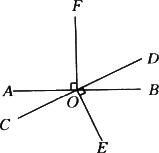
如下图所示，直线AB，CD相交于点O，OE⊥CD，OF⊥AB，∠DOF＝65°，求∠BOE和∠AOC的度数．

Answer 1

答案：
解析：

解：∵AB⊥OF，CD⊥OE(已知)， 　　∴∠BOF＝∠DOE＝90°(垂直定义)． 　　∵∠BOD＝90°－65°＝25°， 　　∴∠BOE＝90°－25°＝65°． 　　∴∠AOC＝∠BOD＝25°(对顶角相等)． 　　分析：由垂直定义可知∠BOF，∠DOE均为90°．可先求∠BOD，再求∠BOE．利用“对顶角相等”这条性质可得∠AOC与∠BOD相等．