题目内容
在“5•12大地震”灾民安置工作中,某企业接到一批生产甲种板材24000 m2和乙种板材12000 m2的任务.(1)已知该企业安排140人生产这两种板材,每人每天能生产甲种板材30 m2或乙种板材20 m2.问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
(2)某灾民安置点计划用该企业生产的这批板材搭建A,B两种型号的板房共400间,在搭建过程中,按实际需要调运这两种板材.已知建一间A型板房和一间B型板房所需板材及能安置的人数如下表所示:
| 板房型号 | 甲种板材 | 乙种板材 | 安置人数 |
| A型板房 | 54m2 | 26m2 | 5 |
| B型板房 | 78m2 | 41m2 | 8 |
分析:(1)设有x人生产甲种板材,那么就有(140-x)人生产乙种板材,根据每人每天能生产甲种板材30 m2或乙种板材20 m2他们用相同的时间完成各自的生产任务,可列方程求解.
(2)设生产A种板房y间,B种板房(400-y)间,根据拥有的甲种板材24000 m2和乙种板材12000m2的材料,和搭建每种一间房所有的材料情况可列出不等式组,可见B越多容纳的人越多.
(2)设生产A种板房y间,B种板房(400-y)间,根据拥有的甲种板材24000 m2和乙种板材12000m2的材料,和搭建每种一间房所有的材料情况可列出不等式组,可见B越多容纳的人越多.
解答:解:(1)设有x人生产甲种板材,
=
x=80.
经检验x=80是分式方程的解.
140-80=60.
故安排80人生产甲种板材,60人生产乙种板材.
(2)设生产A种板房y型,B种板房(400-y)型,
安置人数为5y+8(400-y)=-3y+3200,
,解得:y≥300.
因为-3<0,所以当y=300时安置的人数最多.
300×5+(400-300)×8=2300.
故最多能安置2300人.
| 24000 |
| 30x |
| 12000 |
| 20(140-x) |
x=80.
经检验x=80是分式方程的解.
140-80=60.
故安排80人生产甲种板材,60人生产乙种板材.
(2)设生产A种板房y型,B种板房(400-y)型,
安置人数为5y+8(400-y)=-3y+3200,
|
因为-3<0,所以当y=300时安置的人数最多.
300×5+(400-300)×8=2300.
故最多能安置2300人.
点评:本题考查了分式方程的应用,设出人数,根据时间做为等量关系列出方程求出解,第(2)问中以消耗的木材小于等于拥有的木材做为不等量关系列出不等式组求解,且B房越多,安置的人数越多,可得结果.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在“5•12大地震”灾民安置工作中,某企业接到一批生产甲种板材24000m2和乙种板材12000m2的任务.
(1)已知该企业安排140人生产这两种板材,每人每天能生产甲种板材30m2或乙种板材20m2.问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
(2)某灾民安置点计划用该企业生产的这批板材搭建A,B两种型号的板房共400间,在搭建过程中,按实际需要调运这两种板材.已知建一间A型板房和一间B型板房所需板材及能安置的人数如下表所示:
问:这400间板房最多能安置多少灾民?
(1)已知该企业安排140人生产这两种板材,每人每天能生产甲种板材30m2或乙种板材20m2.问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
(2)某灾民安置点计划用该企业生产的这批板材搭建A,B两种型号的板房共400间,在搭建过程中,按实际需要调运这两种板材.已知建一间A型板房和一间B型板房所需板材及能安置的人数如下表所示:
| 板房型号 | 甲种板材 | 乙种板材 | 安置人数 |
| A型板房 | 54m2 | 26m2 | 6 |
| B型板房 | 78m2 | 41m2 | 9 |
在“5•12大地震”灾民安置工作中,某企业接到一批生产甲种板材24000m2和乙种板材12000m2的任务.
(1)已知该企业安排140人生产这两种板材,每人每天能生产甲种板材30m2或乙种板材20m2,问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
(2)某灾民安置点计划用该企业生产的这批板材搭建A、B两种型号的板房共400间,在搭建过程中,按实际需要调运这两种板材,己知建一间A型板房和一间B型板房所需板材及能安置的人数如下表所示:
问:这400间板房最多能安置多少灾民?
(1)已知该企业安排140人生产这两种板材,每人每天能生产甲种板材30m2或乙种板材20m2,问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
(2)某灾民安置点计划用该企业生产的这批板材搭建A、B两种型号的板房共400间,在搭建过程中,按实际需要调运这两种板材,己知建一间A型板房和一间B型板房所需板材及能安置的人数如下表所示:
| 板房型号 | 甲种板材 | 乙种板材 | 安置人数 |
| A型板房 | 54m2 | 26m2 | 6 |
| B型板房 | 78m2 | 41m2 | 10 |

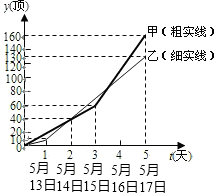 在“5•12大地震”抗震救灾期间,甲、乙两个帐篷生产厂不断提高帐篷生产量.帐篷总产量y(顶)随时间t(天)之间的变化成直线(折线段)上升趋势,如图所示.请你结合图象填空和解答问题:
在“5•12大地震”抗震救灾期间,甲、乙两个帐篷生产厂不断提高帐篷生产量.帐篷总产量y(顶)随时间t(天)之间的变化成直线(折线段)上升趋势,如图所示.请你结合图象填空和解答问题: