��Ŀ����
��ͼ��ʾ��ijѧУ�⽨һ�����ڽӾ��ε����λ�̳����̳Ϊ��Գ�ͼ�Σ������ε��ĸ�����ֱ��������������ϣ�����ABCD�ı߳�AB=4�ף���ABC=60�㣮��AE=x�ף�0��x��4��������EFGH�����ΪS��2��

��1����S��x�ĺ�����ϵʽ��
��2��ѧУ���ھ�������ֲ��ɫ���ݣ��ĸ�����������ֲ��ɫ���ݣ���֪��ɫ���ݵļ۸�Ϊ20Ԫ/��2����ɫ���ݵļ۸�Ϊ40Ԫ/��2����xΪ��ֵʱ������������ܷ�����ͣ����������ܷ��ã�����������ţ���
�⣺��1������AC��BD��

��̳Ϊ��Գ�ͼ�Σ�
��EH��BD��EF��AC��
���BEF�ס�BAC��
�ߡ�ABC=60�㣬
���ABC����BEF�ǵȱ������Ρ�
��EF=BE=AB��AE=4��x��
��Rt��AEM�У���AEM=��ABD=30�㣬
��EM=AEcos��AEM=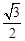 x����EH=2EM=
x����EH=2EM= x.
x.
��S=��4��x���� x=��
x=�� x2+4
x2+4 x��
x��
��2�����������ABCD�����Ϊ8 cm2��
cm2��
�ɣ�1���ã�����ABCD�����Ϊ x2����ɵ��ĸ������ε����Ϊ��8
x2����ɵ��ĸ������ε����Ϊ��8 +
+ x2��4
x2��4 x����
x����
���ܷ���ΪW��
��W=20���� x2+4
x2+4 x��+40��8
x��+40��8 +
+ x2��4
x2��4 x��=20
x��=20 x2��80
x2��80 x+320
x+320
=20 ��x��2��2+240
��x��2��2+240 ��
��
��0��x��4���൱x=2ʱ��Wȡ����С��W��С=240 Ԫ��
Ԫ��
�൱xΪ2ʱ������������ܷ�����ͣ���ͷ���Ϊ240 Ԫ��
Ԫ��
��������
�����������1������AC��BD��������ԳƵ����ʣ��ɵ�EH��BD��EF��AC����BEFΪ�ȱ������Σ��Ӷ����EF����Rt��AEM�����EM���̶��ó�EH���������ɵó�S��x�ĺ�����ϵʽ��
��2�����ݣ�1���Ĵ𰸣�������ĸ������ε�����������ΪW����ɵó�W����x�Ķ��κ�����ϵʽ�������䷽������ֵ���ɡ�

 28����ͼ��ʾ��ijѧУ�⽨����ƽ�еĽ�ѧ¥���������¥���30�ף���A�㿴C�㣬����Ϊ5�㣻��A�㿴D�㣬����Ϊ30�㣬����������⣺
28����ͼ��ʾ��ijѧУ�⽨����ƽ�еĽ�ѧ¥���������¥���30�ף���A�㿴C�㣬����Ϊ5�㣻��A�㿴D�㣬����Ϊ30�㣬����������⣺

