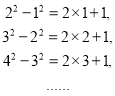Question

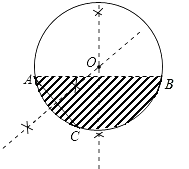
【题目】某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，下图是水平放置的破裂管道有水部分的截面．

（1）请你补全这个输水管道的圆形截面；
（2）若这个输水管道有水部分的水面宽AB=16cm，水面最深地方的高度为4cm，求这个圆形截面的半径．

Answer 1

【答案】
（1）解：先作弦AB的垂直平分线；在弧AB上任取一点C连接AC，作弦AC的垂直平分线，两线交点作为圆心O，OA作为半径，画圆即为所求图形．

（2）解：过O作OE⊥AB于D，交弧AB于E，连接OB．

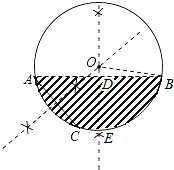
∵OE⊥AB

∴BD= AB= ×16=8cm

由题意可知，ED=4cm

设半径为xcm，则OD=（x﹣4）cm

在Rt△BOD中，由勾股定理得：

OD2+BD2=OB2

∴（x﹣4）2+82=x2

解得x=10．

即这个圆形截面的半径为10cm

【解析】如图所示，根据垂径定理得到BD= AB= ×16=8cm，然后根据勾股定理列出关于圆形截面半径的方程求解．
【考点精析】根据题目的已知条件，利用勾股定理的概念和垂径定理的推论的相关知识可以得到问题的答案，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；推论1：A、平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧B、弦的垂直平分线经过圆心，并且平分弦所对的两条弧C、平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧；推论2 ：圆的两条平行弦所夹的弧相等．