题目内容
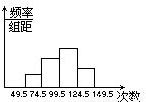
为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试.将所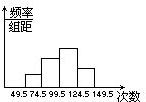 得数据整理后,画出频率分布直方圆如下.已知图中从左到右前三个小组的频率分别为:0.1,0.3,0.4,第一小组的频数为5.
得数据整理后,画出频率分布直方圆如下.已知图中从左到右前三个小组的频率分别为:0.1,0.3,0.4,第一小组的频数为5.(1)求第四小组的频率;
(2)问参加这次测试的学生数是多少?
(3)若次数在75次以上(含75次)为达标,试估计该年级学生跳绳测试的达标率是多少;
(4)问这次测试中,学生跳绳次数的中位数落在四个小组中的哪个小组内?并说明理由.
分析:(1)由频率之和等于1可求得第四组的频率;
(2)由学生总数=第一组的频数÷频率计算;
(3)由于第一组的没有达标,故达标率为
×100%=90%,再用样本估计总体;
(4)由中位数的概念分析.
(2)由学生总数=第一组的频数÷频率计算;
(3)由于第一组的没有达标,故达标率为
| 50-5 |
| 50 |
(4)由中位数的概念分析.
解答:解:(1)∵各小组的频率之和等于1,
∴第四小组的频率为1-(0.1+0.3+0.4)=0.2;
(2)∵第一小组频率为0.1,频数为5,
∴参加这次测试的学生人数为
=50(人);
(3)跳绳测试的达标率为
×100%=90%,
因此,可估计该年级学生跳绳测试的达标率约为90%;
(4)∵第一小组的频数为5,即有5个数据;
第二小组的频数为50×O.3=15,即有15个数据;
第三小组的频数为50×0.4=20,即有20个数据;
将这些数据从小到大排列,位于第25、第26个位置的数据落在第三小组内;
因此,这次测试中,学生跳绳次数的中位数落在第三小组内.
∴第四小组的频率为1-(0.1+0.3+0.4)=0.2;
(2)∵第一小组频率为0.1,频数为5,
∴参加这次测试的学生人数为
| 5 |
| 0.1 |
(3)跳绳测试的达标率为
| 50-5 |
| 50 |
因此,可估计该年级学生跳绳测试的达标率约为90%;
(4)∵第一小组的频数为5,即有5个数据;
第二小组的频数为50×O.3=15,即有15个数据;
第三小组的频数为50×0.4=20,即有20个数据;
将这些数据从小到大排列,位于第25、第26个位置的数据落在第三小组内;
因此,这次测试中,学生跳绳次数的中位数落在第三小组内.
点评:本题考查了频率、中位数的概念和用样本估计总体.注意:各小组的频率之和等于1.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
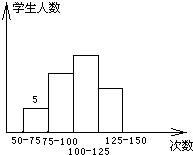 8、为了了解小学生的体能情况,抽取了某小学同年级学生进行跳绳测试,将所得数据整理后,画出如图所示的频数分布直方图,已知图中从左到右前三个小组的频率分别为0.1,0.3,0.4,第一小组的频数为5,则第四小组的频数为
8、为了了解小学生的体能情况,抽取了某小学同年级学生进行跳绳测试,将所得数据整理后,画出如图所示的频数分布直方图,已知图中从左到右前三个小组的频率分别为0.1,0.3,0.4,第一小组的频数为5,则第四小组的频数为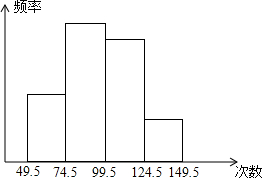 为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数的测试,将所得数据整理后,画出频率分布直方图如图所示.已知图中从左到右前三个小组的频率分别是0.1,0.4,0.3,第一小组的频数为5.
为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数的测试,将所得数据整理后,画出频率分布直方图如图所示.已知图中从左到右前三个小组的频率分别是0.1,0.4,0.3,第一小组的频数为5.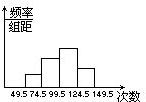 得数据整理后,画出频率分布直方圆如下.已知图中从左到右前三个小组的频率分别为:0.1,0.3,0.4,第一小组的频数为5.
得数据整理后,画出频率分布直方圆如下.已知图中从左到右前三个小组的频率分别为:0.1,0.3,0.4,第一小组的频数为5.