题目内容
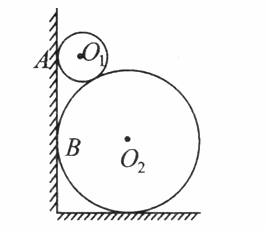
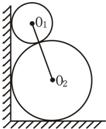
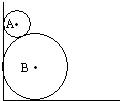 7、如图,两圆轮叠靠在墙边,已知两轮半径分别为4和1,则它们与墙的切点A、B间的距离为( )
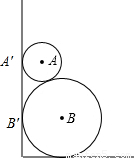
7、如图,两圆轮叠靠在墙边,已知两轮半径分别为4和1,则它们与墙的切点A、B间的距离为( )分析:过A点作AA′垂直墙面,过B点作BB′垂直墙面,过A点作AC⊥BB',求出AC.
解答:解:
过A点作AA′垂直墙面,过B点作BB′垂直墙面,过A点作AC⊥BB',
∵两轮半径分别为4和1,
∴AB=5,BC=3,
∴AC=4,
故墙的切点A、B间的距离为4米,
故选C.

过A点作AA′垂直墙面,过B点作BB′垂直墙面,过A点作AC⊥BB',
∵两轮半径分别为4和1,
∴AB=5,BC=3,
∴AC=4,
故墙的切点A、B间的距离为4米,
故选C.
点评:本题主要考查相切两圆的性质和解直角三角形等知识点.

练习册系列答案
相关题目
 15、如图,两圆轮叠靠在墙边,已知两圆圆心距为7,大圆半径为5,则小圆半径为( )
15、如图,两圆轮叠靠在墙边,已知两圆圆心距为7,大圆半径为5,则小圆半径为( )