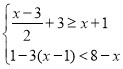题目内容
【题目】如图，在矩形ABCD中，AB=4，AD=6，E是AB边的中点，F是线段BC上的动点，将△EBF沿EF所在直线折叠得到△EB′F，连接B′D，则B′D的最小值是（ ）
A.2
﹣2
B.6
C.2
﹣2
D.4
【答案】A
【解析】解：如图，
当∠BFE=∠DEF，点B′在DE上时，此时B′D的值最小，
根据折叠的性质，△EBF≌△EB′F，
∴EB′⊥FD，
∴EB′=EB，
∵E是AB边的中点，AB=4，
∴AE=EB′=2，
∵AB=6，
∴DE=
=2
，
∴DB′=2﹣2．
故选：A．
【考点精析】关于本题考查的翻折变换（折叠问题），需要了解折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等才能得出正确答案．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某服装店用10000元购进A，B两种新式服装，按标价售出后可获得毛利润5400元（毛利润=售价﹣进价），这两种服装的进价、标价如表所示：
类型、价格 | A型 | B型 |
进价（元/件） | 80 | 100 |
标价（元/件） | 120 | 160 |
（1）这两种服装各购进的件数；
（2）如果A种服装按标价的8折出售，要使这批服装全部售出后毛利润不低于2000元，则B种服装至多按标价的几折出售？
