Question

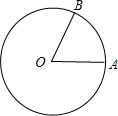如图，将半径为4的圆形纸片沿半径OA、OB将其截成1：5两部分，用所得的扇形围成圆锥的侧面，则圆锥的底面半径为（　　）

• A、2
• B、

  10

  3

• C、

  2

  3

  或

  10

  3

• D、

  1

  3

  或

  5

  3

Answer 1

分析：将半径为4的圆形纸片沿半径OA、OB将其截成1：5两部分，即把360度的圆心角分成了6分份，即分别为60°，300°，用所得的扇形围成圆锥的侧面，可知扇形的弧长就是圆锥的底面周长．

解答：解：圆形被截成了两个扇形，所以有两种围法，一种是大扇形，一种是小扇形，
利用扇形的弧长就是圆锥的底面周长得

60πR

180

=2πr，
解得圆锥的底面半径r=

2

3

；

300πR

180

=2πr，
解得r=

10

3

．
故选C．

点评：注意扇形的弧长就是圆锥的底面，利用弧长等于底面周长的等量关系列式计算．