题目内容
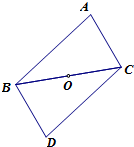21、已知：如图，把△ABC绕边BC的中点O旋转180°得到△DCB．求证：四边形ABDC是平行四边形．
分析：平行四边形的判定方法有多种，选择哪一种解答应先分析题目中给的哪一方面的条件多些，本题所给的条件为△DCB是由△ABC旋转180°所得，根据条件在图形中的位置，可选择利用“对角线相互平分的四边形为平行四边形”来解决．
解答：证明：因为△DCB是由△ABC旋转180°所得，（2分）
所以点A、D，B、C关于点O中心对称，（4分）
所以OB=OC，OA=OD，（6分）
所以四边形ABCD是平行四边形．（8分）
（注：还可以利用旋转变换得到AB=CD，AC=BD相等；或证明△ABC≌△DCB证ABCD是平行四边形．）
所以点A、D，B、C关于点O中心对称，（4分）
所以OB=OC，OA=OD，（6分）
所以四边形ABCD是平行四边形．（8分）
（注：还可以利用旋转变换得到AB=CD，AC=BD相等；或证明△ABC≌△DCB证ABCD是平行四边形．）
点评：平行四边形的判定方法共有五种，应用时要认真领会它们之间的联系与区别，同时要根据条件合理、灵活地选择方法．
练习册系列答案
黎明文化寒假作业系列答案
相关题目
2、已知：如图，把一张矩形纸片ABCD沿BD对折，使C点落在E处，BE与AD相交于点O，写出一组相等的线段
已知：如图，把矩形OCBA放置于直角坐标系中，OC=3，BC=2，取AB的中点M，连接MC，把△MBC沿x轴的负方向平移OC的长度后得到△DAO．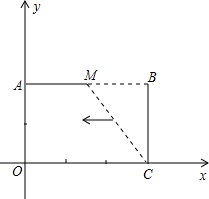
已知：如图，把矩形OCBA放置于直角坐标系中，OC=3，BC=2，取AB的中点M，连结MC，把△MBC沿x轴的负方向平移OC的长度后得到△DAO．
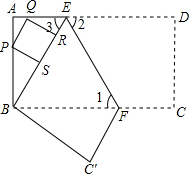已知：如图，把长方形纸片ABCD沿EF折叠后，点D与点B重合，点C落在点C′的位置上．若∠1=60°，AE=1．