题目内容
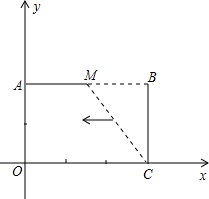 已知:如图,把矩形OCBA放置于直角坐标系中,OC=3,BC=2,取AB的中点M,连结MC,把△MBC沿x轴的负方向平移OC的长度后得到△DAO.
已知:如图,把矩形OCBA放置于直角坐标系中,OC=3,BC=2,取AB的中点M,连结MC,把△MBC沿x轴的负方向平移OC的长度后得到△DAO.(1)直接写出点D的坐标;
(2)已知点B与点D在经过原点的抛物线上,点P在第一象限内的该抛物线上移动,过点P作PQ⊥x轴于点Q,连结OP.若以O、P、Q为顶点的三角形与△DAO相似,试求出点P的坐标.
分析:(1)由矩形的性质,平移的性质以及中点的定义可得DA=MB=
AB=
,OA=BC=2,∠DAO=∠B=90°,进而求出点D的坐标;
(2)先由抛物线经过原点,可设抛物线的解析式为y=ax2+bx(a≠0),再将B(3,2)与点D(-
,2)代入,运用待定系数法求出抛物线的解析式为y=
x2-
x,则点P的坐标可设为(x,
x2-
x).因为∠OQP=∠OAD=90°,所以当以O、P、Q为顶点的三角形与△DAO相似时,Q与A一定对应,然后分两种情况进行讨论:(i)△PQO∽△DAO;(ii)△OQP∽△DAO.根据相似三角形对应边成比例列出比例式,求解即可.
| 1 |
| 2 |
| 3 |
| 2 |
(2)先由抛物线经过原点,可设抛物线的解析式为y=ax2+bx(a≠0),再将B(3,2)与点D(-
| 3 |
| 2 |
| 4 |
| 9 |
| 2 |
| 3 |
| 4 |
| 9 |
| 2 |
| 3 |
解答: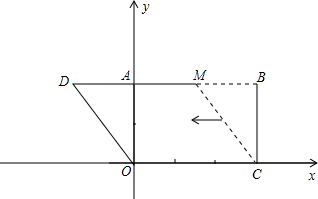 解:(1)∵四边形OCBA是矩形,
解:(1)∵四边形OCBA是矩形,
∴AB=OC=3,OA=BC=2,∠B=90°.
∵M是AB的中点,
∴AM=MB=
AB=
.
∵把△MBC沿x轴的负方向平移OC的长度后得到△DAO,
∴DA=MB=
,∠DAO=∠B=90°,
∴点D的坐标为(-
,2);
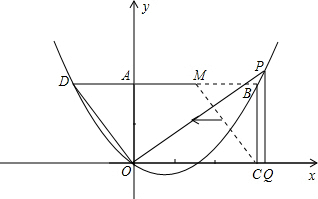 (2)∵OC=3,BC=2,∴B(3,2).
(2)∵OC=3,BC=2,∴B(3,2).
∵抛物线经过原点,
∴设抛物线的解析式为y=ax2+bx(a≠0),
又抛物线经过点B(3,2)与点D(-
,2),
∴
,解得:
,
∴抛物线的解析式为y=
x2-
x.
∵点P在抛物线上,
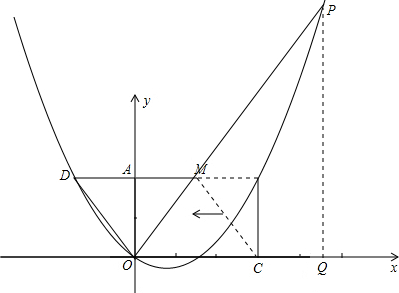 ∴设点P的坐标为(x,
∴设点P的坐标为(x,
x2-
x).
分两种情况:
(i)若△PQO∽△DAO,则
=
,
即
=
,解得:x1=0(舍去),x2=
,
∴点P的坐标为(
,
);
(ii)若△OQP∽△DAO,则
=
,
即
=
,解得:x1=0(舍去),x2=
,
∴点P的坐标为(
,6).
 解:(1)∵四边形OCBA是矩形,
解:(1)∵四边形OCBA是矩形,∴AB=OC=3,OA=BC=2,∠B=90°.
∵M是AB的中点,
∴AM=MB=
| 1 |
| 2 |
| 3 |
| 2 |
∵把△MBC沿x轴的负方向平移OC的长度后得到△DAO,
∴DA=MB=
| 3 |
| 2 |
∴点D的坐标为(-
| 3 |
| 2 |
 (2)∵OC=3,BC=2,∴B(3,2).
(2)∵OC=3,BC=2,∴B(3,2).∵抛物线经过原点,
∴设抛物线的解析式为y=ax2+bx(a≠0),
又抛物线经过点B(3,2)与点D(-
| 3 |
| 2 |
∴
|
|
∴抛物线的解析式为y=
| 4 |
| 9 |
| 2 |
| 3 |
∵点P在抛物线上,
 ∴设点P的坐标为(x,
∴设点P的坐标为(x,| 4 |
| 9 |
| 2 |
| 3 |
分两种情况:
(i)若△PQO∽△DAO,则
| PQ |
| DA |
| QO |
| AO |
即
| ||||
|
| x |
| 2 |
| 51 |
| 16 |
∴点P的坐标为(
| 51 |
| 16 |
| 153 |
| 64 |
(ii)若△OQP∽△DAO,则
| OQ |
| DA |
| PQ |
| AO |
即
| x | ||
|
| ||||
| 2 |
| 9 |
| 2 |
∴点P的坐标为(
| 9 |
| 2 |
点评:本题考查了二次函数的综合题型,其中涉及到的知识点有运用待定系数法求抛物线的解析式,矩形、平移的性质,相似三角形的判定与性质,综合性较强,难度适中.运用数形结合及分类讨论是解题的关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 已知:如图,把矩形OCBA放置于直角坐标系中,OC=3,BC=2,取AB的中点M,连接MC,把△MBC沿x轴的负方向平移OC的长度后得到△DAO.
已知:如图,把矩形OCBA放置于直角坐标系中,OC=3,BC=2,取AB的中点M,连接MC,把△MBC沿x轴的负方向平移OC的长度后得到△DAO.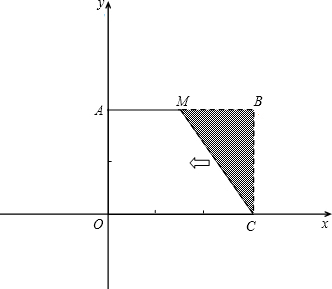 点M,连接MC,把△MBC沿x轴的负方向平移OC的长度后得到△DAO.
点M,连接MC,把△MBC沿x轴的负方向平移OC的长度后得到△DAO.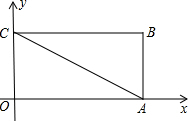 ,并且OC>OE.
,并且OC>OE.