Question

如图，点C为线段BD上一动点，分别过点B、D作AB⊥BD，ED⊥BD，连接AC、EC。已知AB=5，DE=1，
BD=8，设CD=x。

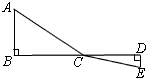
（1）用含x的代数式表示AC+CE的长；
（2）请问点C满足什么条件时，AC+CE的值最小?
（3）根据（2）中的规律和结论，请构图求出代数式的最小值。

Answer 1

解：（1）∵AB⊥BD，ED⊥BD，                 且AB=5，ED=1，BD=8，CD=x，    ∴，        ，    ∴。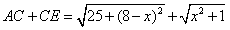
（2）当C点在线段BD与线段AE的交点处的时候，AC+CE的值最小。
（3）如图，AB⊥BD，ED⊥BD，AE与BD交于点C，   AB=3，DE=2，BD=12，设CD=x，   过E点作BD的平行线交AB延长线于F点， 由（2）可知代数式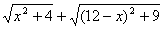的最小值就是线段AE长，   在Rt△AFE中，∠AFE=90°，   AF=AB+DE=3+2=5，EF=BD=12，   ，    ∴代数式的最小值是13。