题目内容
【题目】如图,在平面直角坐标系xOy中,多边形OABCDE的顶点坐标为O(0,0),A(2,0),B(2,2),C(4,2),D(4,4),E(0,4),若如图过点M(1,2)的直线MP(与y轴交于点P)将多边形OABCDE分割成面积相等的两部分,则直线MP的函数表达式是___________.

【答案】![]()
【解析】延长CB交y轴于点F,如图所示:
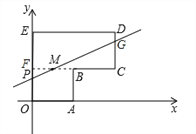
∵A(2,0),B(2,2),C(4,2),D(4,4),E(0,4),
∴S正方形OABF=OAAB=2×2=4,
S矩形CDEF=CFCD=4×2=8,
∴S多边形OABCDE=4+8=12,
设直线PG的解析式为y=kx+b(k≠0),
∵M(1,2),
∴k+b=2①,
∵点P在y轴上,
∴P(0,b),
∵C(4,2),D(4,4),
∴G(4,4k+b),
∴S梯形PGDE=![]() (DG+PE)DE=
(DG+PE)DE=![]() S多边形OABCDE=
S多边形OABCDE=![]() ×(4-4k-b+4-b)×4=6,即8k+4b=10②,
×(4-4k-b+4-b)×4=6,即8k+4b=10②,
①②联立得,![]() ,
,
解得![]() ,
,
故此一次函数的解析式为:y=![]() x+
x+![]() 。
。
故答案是:y=![]() x+
x+![]() 。
。

练习册系列答案
相关题目