题目内容
如图,菱形ABCD中,BE⊥AD于点E,AC交BE于点F,连接DF,AD=5,BE=4.动点P从点A出发,沿折线A-D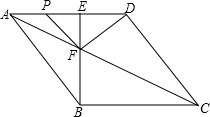 -C方向以1个单位/秒的速度向终点C匀速运动,点P的运动时间为t秒.
-C方向以1个单位/秒的速度向终点C匀速运动,点P的运动时间为t秒.
(1)请求出线段EF的长度;
(2)设PF2=y,请直接写出y与t之间的函数关系式,并写出自变量t的取值范围;
(3)在点P的运动过程中,若∠FPD与∠BCD互余,求此时直线BP与直线AC所夹锐角的正切值.
 -C方向以1个单位/秒的速度向终点C匀速运动,点P的运动时间为t秒.
-C方向以1个单位/秒的速度向终点C匀速运动,点P的运动时间为t秒.(1)请求出线段EF的长度;
(2)设PF2=y,请直接写出y与t之间的函数关系式,并写出自变量t的取值范围;
(3)在点P的运动过程中,若∠FPD与∠BCD互余,求此时直线BP与直线AC所夹锐角的正切值.
分析:(1)由菱形的“四条边相等,对边互相平行的性质以及勾股定理”求得AE=3.然后根据相似三角形(△AEF∽△CBF)的对应边成比例列出比例式
=
,即
=
,易求EF的长度;
(2)分P在AD上和P在CD上两种情况进行讨论,当0≤t≤5时,在直角△EFP中利用勾股定理即可求得;当5<t≤10时,作CD的垂线BM,在直角△BMP中,利用勾股定理即可求得函数的解析式;
(3)若∠BCD+∠FPD=90°,易证△ABF≌△ADF,则∠3=∠ABE=∠FPD,当点P在AD上时可以证得△APG∽△CBG,根据相似三角形的对应边的比相等即可求得AG的长,进而得到OG的长,根据三角函数的定义求解;当点P在CD上时,易证△ABG∽△CPG,根据相似三角形的对应边相等即可求得CG的长,进而得到OG的长,然后利用三角函数的定义即可求解.
| AE |
| BC |
| EF |
| BF |
| 3 |
| 5 |
| EF |
| 4-EF |
(2)分P在AD上和P在CD上两种情况进行讨论,当0≤t≤5时,在直角△EFP中利用勾股定理即可求得;当5<t≤10时,作CD的垂线BM,在直角△BMP中,利用勾股定理即可求得函数的解析式;
(3)若∠BCD+∠FPD=90°,易证△ABF≌△ADF,则∠3=∠ABE=∠FPD,当点P在AD上时可以证得△APG∽△CBG,根据相似三角形的对应边的比相等即可求得AG的长,进而得到OG的长,根据三角函数的定义求解;当点P在CD上时,易证△ABG∽△CPG,根据相似三角形的对应边相等即可求得CG的长,进而得到OG的长,然后利用三角函数的定义即可求解.
解答: 解:(1)∵四边形ABCD是菱形,
解:(1)∵四边形ABCD是菱形,
∴AB=AD=BC=CD=5,AD∥BC,AB∥CD.
∵BE⊥AD,
∴在Rt△ABE中,AE=
=
=3.
∵AD∥BC,
∴△AEF∽△CBF,
∴
=
,即
=
,
∴EF=
;
(2)当0≤t≤5时,y=(t-3)2+
.
当5<t≤10时,y=(t-5)2+
.
(3)连接BP交AC于点G,连接BD交AC于点O.
在Rt△BED中,BD=
=2
,
∵菱形ABCD,
∴∠BCD=∠BAD,∠1=∠2,BD⊥AC.BO=OD=
,AO=CO,
∴Rt△AOD中,AO=
=2
=CO.
∴Rt△ABE中,∠ABE+∠BAD=90°,
∴若∠BCD+∠FPD=90°,则∠FPD=∠ABE,
在△ABF和△ADF中,
∴△ABF≌△ADF,
∴∠3=∠ABE=∠FPD,
当点P在AD上时,∵∠3=∠FPD,
∴PF=DF
∵EF⊥PD,
∴PE=DE=2,
∵AD∥BC
∴△APG∽△CBG,
∴
=
,即
=
,
∴AG=
,
∴OG=
,
∴Rt△BOG中,tan∠BGO=
=
=
,
∵菱形ABCD中,BE⊥AD,∠ACB=∠ACD,
∴BE⊥BC,即∠FBC=90°,
在△BCF和△DCF中,
,
∴△BCF≌△DCF,
∴∠FED=∠FDP=90°
又∵当点P在CD上时,∠3=∠FPD,
∴△FED∽△FDP,
∴
=
,即
=
,
∴DP=
,
∴CP=
,
∵AB∥CD,
∴△ABG∽△CPG,
∴
=
,即
=
,
∴CG=
=OG,
∴Rt△BOG中,tan∠BGO=
=
=1.
 解:(1)∵四边形ABCD是菱形,
解:(1)∵四边形ABCD是菱形,∴AB=AD=BC=CD=5,AD∥BC,AB∥CD.
∵BE⊥AD,
∴在Rt△ABE中,AE=
| AB2-BE2 |
| 52-42 |
∵AD∥BC,
∴△AEF∽△CBF,
∴
| AE |
| BC |
| EF |
| BF |
| ||
|
| EF |
| 4-EF |
∴EF=
| 3 |
| 2 |
(2)当0≤t≤5时,y=(t-3)2+
| 9 |
| 4 |
当5<t≤10时,y=(t-5)2+
| 25 |
| 4 |
(3)连接BP交AC于点G,连接BD交AC于点O.
在Rt△BED中,BD=
| DE2+BE2 |
| 5 |
∵菱形ABCD,
∴∠BCD=∠BAD,∠1=∠2,BD⊥AC.BO=OD=
| 5 |
∴Rt△AOD中,AO=
| AD2-OD2 |
| 5 |
∴Rt△ABE中,∠ABE+∠BAD=90°,
∴若∠BCD+∠FPD=90°,则∠FPD=∠ABE,
在△ABF和△ADF中,
|
∴△ABF≌△ADF,
∴∠3=∠ABE=∠FPD,
当点P在AD上时,∵∠3=∠FPD,
∴PF=DF
∵EF⊥PD,
∴PE=DE=2,

∵AD∥BC
∴△APG∽△CBG,
∴
| AP |
| CB |
| AG |
| CG |
| 1 |
| 5 |
| AG | ||
4
|
∴AG=
2
| ||
| 3 |
∴OG=
4
| ||
| 3 |
∴Rt△BOG中,tan∠BGO=
| OB |
| OG |
| ||||
|
| 3 |
| 4 |
∵菱形ABCD中,BE⊥AD,∠ACB=∠ACD,
∴BE⊥BC,即∠FBC=90°,
在△BCF和△DCF中,
|
∴△BCF≌△DCF,
∴∠FED=∠FDP=90°
又∵当点P在CD上时,∠3=∠FPD,
∴△FED∽△FDP,
∴
| FE |
| FD |
| ED |
| DP |
| 3 |
| 5 |
| 2 |
| DP |
∴DP=
| 10 |
| 3 |
∴CP=
| 5 |
| 3 |
∵AB∥CD,
∴△ABG∽△CPG,
∴
| CP |
| AB |
| CG |
| AG |
| ||
| 5 |
| CG | ||
4
|
∴CG=
| 5 |
∴Rt△BOG中,tan∠BGO=
| OB |
| OG |
| ||
|
点评:本题考查了菱形、三角形全等、三角形相似的综合应用,正确证得三角形相似是关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
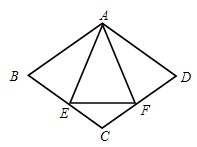 26、已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.
26、已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.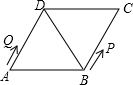 如图,菱形ABCD中,∠A=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿B→C→D向终点D运动.同时动点Q从点A出发,以相同的速度沿A→D→B向终点B运动,运动的时间为x秒,当点P到达点D时,点P、Q同时停止运动,设△APQ的面积为y,则反映y与x的函数关系的图象是( )
如图,菱形ABCD中,∠A=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿B→C→D向终点D运动.同时动点Q从点A出发,以相同的速度沿A→D→B向终点B运动,运动的时间为x秒,当点P到达点D时,点P、Q同时停止运动,设△APQ的面积为y,则反映y与x的函数关系的图象是( )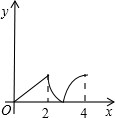
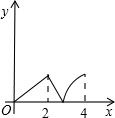
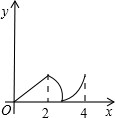
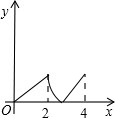
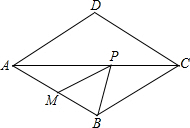 如图,菱形ABCD中,∠BAD=60°,M是AB的中点,P是对角线AC上的一个动点,若AB长为2
如图,菱形ABCD中,∠BAD=60°,M是AB的中点,P是对角线AC上的一个动点,若AB长为2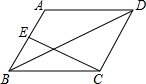 如图:菱形ABCD中,E是AB的中点,且CE⊥AB,AB=6cm.
如图:菱形ABCD中,E是AB的中点,且CE⊥AB,AB=6cm. 如图,菱形ABCD中,∠ADC=120°,AB=10,
如图,菱形ABCD中,∠ADC=120°,AB=10,