题目内容
（2012•深圳模拟）若⊙O1和⊙O2相交于点A、B，且AB=24，⊙O1的半径为13，⊙O2的半径为15，则O1O2的长为
14
14
或4
4
．（有两解）分析：根据两圆相交，可知为O1O2⊥AB且AC=BC，然后利用已知条件和勾股定理求解．
解答：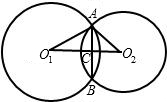
解：如图，连接O1O2，交AB于C，
∴O1O2⊥AB，
∴AC=12，O1A=13，
∴O1C=
=5；
∵O2A=15，AC=12，
∴O2C=
=9，
因此O1O2=5+9=14．
同理知当小圆圆心在大圆内时，解得O1O2=4．
故答案为14或4．
解：如图，连接O1O2，交AB于C，∴O1O2⊥AB，
∴AC=12，O1A=13，
∴O1C=
| O1A2-AC2 |
∵O2A=15，AC=12，
∴O2C=
| O2A2-AC2 |
因此O1O2=5+9=14．
同理知当小圆圆心在大圆内时，解得O1O2=4．
故答案为14或4．
点评：本题主要考查了圆与圆的位置关系，勾股定理等知识点．本题可以通过构建直角三角形，然后来求解．
练习册系列答案
相关题目
（2012•深圳模拟）如图，将一把两边都带有刻度的直尺放在半圆形纸片上，使其一边经过圆心O，另一边所在直线与半圆相交于点D、E，量出半径OC=5cm，弦DE=8cm，则直尺的宽度