题目内容
【题目】如图,![]() 为△ABC内任意一点,若将△ABC作平移变换,使A点落在B点的位置上,已知A(3,4);B(-2,2);C(2,-2).
为△ABC内任意一点,若将△ABC作平移变换,使A点落在B点的位置上,已知A(3,4);B(-2,2);C(2,-2).

(1) 请直接写出B点、C点、P点的对应点B1,C1,P1的坐标;
(2) 求△AOC的面积S△AOC.
【答案】(1) B1(-7,0),C1(-3,-4),P1(x0-5,y0-2) ;(2) 7.
【解析】
(1)由点A及其对应点的坐标得出平移的方向和距离,根据平移变换点的坐标变化规律可得;
(2)利用割补法求解可得.
解:(1)由A(3,4)平移到B(-2,2),所以需要将△ABC向左平移5个单位,向下平移2个单位,即横坐标减5,纵坐标减2.
∴点B的对应点的坐标为B1(-7,0),点C的对应点的坐标为C1(-3,-4),点P的对应点的坐标P1 (x0-5,y0-2)
(2)连接OA,作AD⊥y轴于D,CE⊥y轴于E
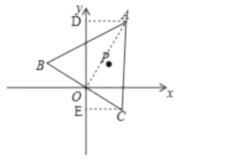
则:AD=3,OD=4,OE=2,CE=2,DE=6
∴S△AOC=S梯形ADEC-S△AOD-S△COE
![]()
=15-6-2=7

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目