题目内容
 把自然数按上小下大、左小右大的原则排成如图的三角形数表(每行比上一行多一个数).设aij(i、j∈N+)是位于这个三角形数表中从上往下数第i行、从左往右数的第j个数(如a42=8).
把自然数按上小下大、左小右大的原则排成如图的三角形数表(每行比上一行多一个数).设aij(i、j∈N+)是位于这个三角形数表中从上往下数第i行、从左往右数的第j个数(如a42=8).(1)若aij=2010,求i、j的值.
(2)记三角形数表从上往下数第n行各数的和为bn,令cn=
|
分析:(1)三角形数表中前n行共有1+2+…+n=
个,即第i行的最后一个数是
.
因此,使aij=2010的i是不等式
≥2010的最小正整数解.
(2)先求出前n行的所有自然数的和,从而得出bn,代入即可求得cn,Tn.
| n(n+1) |
| 2 |
| i(i+1) |
| 2 |
因此,使aij=2010的i是不等式
| i(i+1) |
| 2 |
(2)先求出前n行的所有自然数的和,从而得出bn,代入即可求得cn,Tn.
解答:解:(1)因为
=1953,
而
=2016,所以i=63.
于是,第63行的第一个数是
+1=1954.
故j=(2010-1954)+1=57.
(2)前n行的所有自然数的和为Sn=
×
[
+1]=
.
则bn=Sn-Sn-1=
,
所以当n≥2时,cn=
=
-
,
∴Tn=
-
-
.
| 62×63 |
| 2 |
而
| 63×64 |
| 2 |
于是,第63行的第一个数是
| 62×63 |
| 2 |
故j=(2010-1954)+1=57.
(2)前n行的所有自然数的和为Sn=
| 1 |
| 2 |
| n(n+1) |
| 2 |
| n(n+1) |
| 2 |
| n(n+1)(n2+n+2) |
| 8 |
则bn=Sn-Sn-1=
| n(n2+1) |
| 2 |
所以当n≥2时,cn=
| n |
| bn-n |
| 1 |
| n-1 |
| 1 |
| n+1 |
∴Tn=
| 5 |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
点评:本题考查了规律型:数字的变化,注意三角形数表中前n行共有1+2+…+n=
个,即第i行的最后一个数是
,依此解题.
| n(n+1) |
| 2 |
| i(i+1) |
| 2 |

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目

 把自然数按上小下大、左小右大的原则排成如图的三角形数表(每行比上一行多一个数).设aij(i、j∈N+)是位于这个三角形数表中从上往下数第i行、从左往右数的第j个数(如a42=8).
把自然数按上小下大、左小右大的原则排成如图的三角形数表(每行比上一行多一个数).设aij(i、j∈N+)是位于这个三角形数表中从上往下数第i行、从左往右数的第j个数(如a42=8).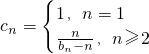 .若数列{cn}的前n项和为Tn,求Tn.
.若数列{cn}的前n项和为Tn,求Tn.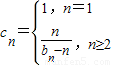 .若数列{cn}的前n项和为Tn,求Tn.
.若数列{cn}的前n项和为Tn,求Tn.