题目内容
把自然数按上小下大、左小右大的原则排成如图的三角形数表(每行比上一行多一个数).设aij(i、j是正整数)是位于这个三角形数表中从上往下数第i行、从左往右数的第j个数(如a42=8).
(1)若aij=2008,求i、j的值.
(2)记三角形数表从上往下数第n行各数的和为bn,令
若数列{Cn}的前n项和为Tn,求Tn.
【答案】
(1)i=63j=55(2)Tn=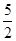 -
-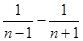 .
.
【解析】
试题分析:(1)三角形数表中前n行共有:1+2+…+n=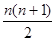 个,即第i行的最后一个数是
个,即第i行的最后一个数是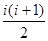 .
.
因此,使aij=2008的i是不等式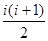 ≥2008的最小正整数解.
≥2008的最小正整数解.
因为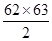 =1953,而
=1953,而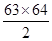 =2016,所以,i=63.于是,第63行的第一个数是
=2016,所以,i=63.于是,第63行的第一个数是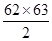 +1=1954.故j=(2008—1954)+1=55.
+1=1954.故j=(2008—1954)+1=55.
(2)前n行的所有自然数的和为
Sn=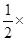
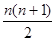 =
=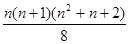
则bn=Sn-Sn-1=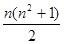 ,∴当n≥2时,
,∴当n≥2时,
Tn=1+(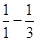 )+(
)+(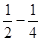 )+(
)+(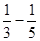 )+…+(
)+…+(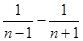 )
)
=1+1+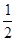 -
-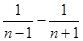 =
=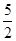 -
-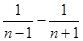 .
.
考点:规律探究题
点评:本题难度较大,主要考查学生根据已知条件归纳总结一般规律的能力。探究规律题型为中考常考题型,要求学生多做训练,掌握解题技巧并运用到考试中去。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 把自然数按上小下大、左小右大的原则排成如图的三角形数表(每行比上一行多一个数).设aij(i、j∈N+)是位于这个三角形数表中从上往下数第i行、从左往右数的第j个数(如a42=8).
把自然数按上小下大、左小右大的原则排成如图的三角形数表(每行比上一行多一个数).设aij(i、j∈N+)是位于这个三角形数表中从上往下数第i行、从左往右数的第j个数(如a42=8). 把自然数按上小下大、左小右大的原则排成如图的三角形数表(每行比上一行多一个数).设aij(i、j∈N+)是位于这个三角形数表中从上往下数第i行、从左往右数的第j个数(如a42=8).
把自然数按上小下大、左小右大的原则排成如图的三角形数表(每行比上一行多一个数).设aij(i、j∈N+)是位于这个三角形数表中从上往下数第i行、从左往右数的第j个数(如a42=8).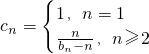 .若数列{cn}的前n项和为Tn,求Tn.
.若数列{cn}的前n项和为Tn,求Tn.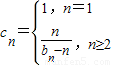 .若数列{cn}的前n项和为Tn,求Tn.
.若数列{cn}的前n项和为Tn,求Tn.