题目内容
知识迁移
当a>0且x>0时,因为(
-
)2≥0,所以x-2
+
≥0,从而x+
≥2
(当x=
)是取等号).
记函数y=x+
(a>0,x>0).由上述结论可知:当x=
时,该函数有最小值为2
.
直接应用
已知函数y1=x(x>0)与函数y2=
(x>0),则当x=______时,y1+y2取得最小值为______.
变形应用
已知函数y1=x+1(x>-1)与函数y2=(x+1)2+4(x>-1),求
的最小值,并指出取得该最小值时相应的x的值.
实际应用
已知某汽车的一次运输成本包含以下三个部分,一是固定费用,共360元;二是燃油费,每千米1.6元;三是折旧费,它与路程的平方成正比,比例系数为0.001.设该汽车一次运输的路程为x千米,求当x为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
当a>0且x>0时,因为(
| x |
| ||
|
| a |
| a |
| x |
| a |
| x |
| a |
| a |
记函数y=x+
| a |
| x |
| a |
| a |
直接应用
已知函数y1=x(x>0)与函数y2=
| 1 |
| x |
变形应用
已知函数y1=x+1(x>-1)与函数y2=(x+1)2+4(x>-1),求
| y2 |
| y1 |
实际应用
已知某汽车的一次运输成本包含以下三个部分,一是固定费用,共360元;二是燃油费,每千米1.6元;三是折旧费,它与路程的平方成正比,比例系数为0.001.设该汽车一次运输的路程为x千米,求当x为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
直接应用:
∵函数y=x+
(a>0,x>0),由上述结论可知:当x=
时,该函数有最小值为2
.
∴函数y1=x(x>0)与函数y2=
(x>0),则当x=1时,y1+y2取得最小值为2.
变形应用
已知函数y1=x+1(x>-1)与函数y2=(x+1)2+4(x>-1),
则
=
=(x+1)+
的最小值为:2
=4,
∵当(x+1)+
=4时,
整理得出:x2-2x+1=0,
解得:x1=x2=1,
检验:x=1时,x+1=2≠0,
故x=1是原方程的解,
故
的最小值为4,相应的x的值为1;
实际应用
设行驶x千米的费用为y,则由题意得,y=360+1.6x+0.001x2,
故平均每千米的运输成本为:
=0.001x+
+1.6=0.001x+
+1.6,
由题意可得:当0.001x=
时,
取得最小,此时x=600km,
此时
≥2
+1.6=2.8,
即当一次运输的路程为600千米时,运输费用最低,最低费用为:2.8元.
答:汽车一次运输的路程为600千米,平均每千米的运输成本最低,最低是2.8元.
∵函数y=x+
| a |
| x |
| a |
| a |
∴函数y1=x(x>0)与函数y2=
| 1 |
| x |
变形应用
已知函数y1=x+1(x>-1)与函数y2=(x+1)2+4(x>-1),
则
| y2 |
| y1 |
| (x+1) 2+4 |
| x+1 |
| 4 |
| x+1 |
| 4 |
∵当(x+1)+
| 4 |
| x+1 |
整理得出:x2-2x+1=0,
解得:x1=x2=1,
检验:x=1时,x+1=2≠0,
故x=1是原方程的解,
故
| y2 |
| y1 |
实际应用
设行驶x千米的费用为y,则由题意得,y=360+1.6x+0.001x2,
故平均每千米的运输成本为:
| y |
| x |
| 360 |
| x |
| 0.36 |
| 0.001x |
由题意可得:当0.001x=
| 0.36 |
| y |
| x |
此时
| y |
| x |
| 0.36 |
即当一次运输的路程为600千米时,运输费用最低,最低费用为:2.8元.
答:汽车一次运输的路程为600千米,平均每千米的运输成本最低,最低是2.8元.

练习册系列答案
相关题目
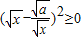 ,所以x-
,所以x-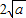 +
+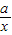 ≥0,从而x+
≥0,从而x+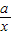 ≥
≥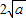 (当x=
(当x=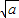 )是取等号).
)是取等号).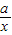 (a>0,x>0).由上述结论可知:当x=
(a>0,x>0).由上述结论可知:当x=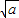 时,该函数有最小值为2
时,该函数有最小值为2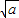 .
.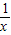 (x>0),则当x=______时,y1+y2取得最小值为______.
(x>0),则当x=______时,y1+y2取得最小值为______.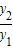 的最小值,并指出取得该最小值时相应的x的值.
的最小值,并指出取得该最小值时相应的x的值.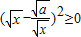 ,所以x-
,所以x-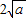 +
+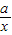 ≥0,从而x+
≥0,从而x+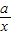 ≥
≥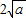 (当x=
(当x=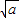 )是取等号).
)是取等号).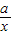 (a>0,x>0).由上述结论可知:当x=
(a>0,x>0).由上述结论可知:当x=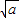 时,该函数有最小值为2
时,该函数有最小值为2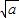 .
.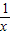 (x>0),则当x=______时,y1+y2取得最小值为______.
(x>0),则当x=______时,y1+y2取得最小值为______.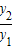 的最小值,并指出取得该最小值时相应的x的值.
的最小值,并指出取得该最小值时相应的x的值.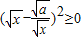 ,所以x-
,所以x- +
+ ≥0,从而x+
≥0,从而x+ ≥
≥ (当x=
(当x= )是取等号).
)是取等号). (a>0,x>0).由上述结论可知:当x=
(a>0,x>0).由上述结论可知:当x= 时,该函数有最小值为2
时,该函数有最小值为2 .
. (x>0),则当x=______时,y1+y2取得最小值为______.
(x>0),则当x=______时,y1+y2取得最小值为______. 的最小值,并指出取得该最小值时相应的x的值.
的最小值,并指出取得该最小值时相应的x的值.