题目内容
如图，上午8：00时，一船在某灯塔O的正东方向5海里的A处向正北方向航行，上午10：00，船离灯塔O的距离MO=13海里，求此船航行的速度．分析：在RT△OAM中，利用勾股定理求出AM的长度，从而根据速度公式可得出船航行的速度．
解答：解：由题意得，OA=5海里，OM=13海里，
在RT△OAM中，AM=
=12海里，
∵航行了2小时，
∴船航行的速度=
=6海里/时．
答：此船的航行速度为：6海里/时．
在RT△OAM中，AM=
| OM2-OA2 |
∵航行了2小时，
∴船航行的速度=
| 12 |
| 2 |
答：此船的航行速度为：6海里/时．
点评：此题考查了勾股定理的应用，解答本题的关键是利用勾股定理求出AM的长度，注意掌握勾股定理的表达式．
练习册系列答案
相关题目
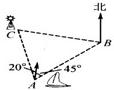16、如图，上午7：00，一船从A港出发，以20km/h的速度向东北方向行驶．经2时，船行驶至B处，此时灯塔C在B处的北偏西85°方向．已知灯塔C在A港的北偏西20°方向，则B，C两处的距离为
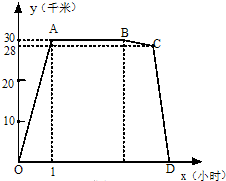23、周六上午8：O0小明从家出发，乘车1小时到郊外某基地参加社会实践活动，在基地活动2.2小时后，因家里有急事，他立即按原路以4千米/时的平均速度步行返回．同时爸爸开车从家出发沿同一路线接他，在离家28千米处与小明相遇．接到小明后保持车速不变，立即按原路返回．设小明离开家的时间为x小时，小明离家的路程y（干米）与x（小时）之间的函致图象如图所示，
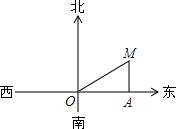如图，上午8：00时，一船在某灯塔O的正东方向5海里的A处向正北方向航行，上午10：00，船离灯塔O的距离MO=13海里，求此船航行的速度．
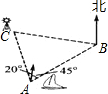如图，上午7：00，一船从A港出发，以20km/h的速度向东北方向行驶．经2时，船行驶至B处，此时灯塔C在B处的北偏西85°方向．已知灯塔C在A港的北偏西20°方向，则B，C两处的距离为________km．