题目内容
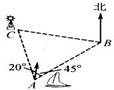 16、如图,上午7:00,一船从A港出发,以20km/h的速度向东北方向行驶.经2时,船行驶至B处,此时灯塔C在B处的北偏西85°方向.已知灯塔C在A港的北偏西20°方向,则B,C两处的距离为
16、如图,上午7:00,一船从A港出发,以20km/h的速度向东北方向行驶.经2时,船行驶至B处,此时灯塔C在B处的北偏西85°方向.已知灯塔C在A港的北偏西20°方向,则B,C两处的距离为40
km.分析:先根据题意画出图形,再根据平行线的性质及等腰三角形的判定定理解答即可.
解答:解:如图所示:
∵∠CAF=20°,∠FAE=45°,AB=2×20=40km,∴∠CAB=65°,
∴∠BAE=90°-45°=45°,
∵BD∥AE,∴∠ABD=45°,
∵∠1=85°,∴∠DBC=90°-85°=5°,∴∠ABC=45°+5°=50°,
∴∠BAC=180°-∠CAB-∠ABC=180°-65°-50°=65°,
∴BC=AB=40km.

∵∠CAF=20°,∠FAE=45°,AB=2×20=40km,∴∠CAB=65°,
∴∠BAE=90°-45°=45°,
∵BD∥AE,∴∠ABD=45°,
∵∠1=85°,∴∠DBC=90°-85°=5°,∴∠ABC=45°+5°=50°,
∴∠BAC=180°-∠CAB-∠ABC=180°-65°-50°=65°,
∴BC=AB=40km.

点评:此题考查的是直角三角形在实际生活中的运用,解答此题的关键是根据题意画出图形,再利用平行线的性质及直角三角形的性质解答.

练习册系列答案
相关题目
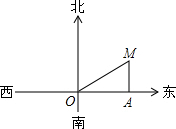 如图,上午8:00时,一船在某灯塔O的正东方向5海里的A处向正北方向航行,上午10:00,船离灯塔O的距离MO=13海里,求此船航行的速度.
如图,上午8:00时,一船在某灯塔O的正东方向5海里的A处向正北方向航行,上午10:00,船离灯塔O的距离MO=13海里,求此船航行的速度. 如图,上午8:00时,一船在某灯塔O的正东方向5海里的A处向正北方向航行,上午10:00,船离灯塔O的距离MO=13海里,求此船航行的速度.
如图,上午8:00时,一船在某灯塔O的正东方向5海里的A处向正北方向航行,上午10:00,船离灯塔O的距离MO=13海里,求此船航行的速度.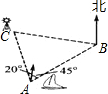 如图,上午7:00,一船从A港出发,以20km/h的速度向东北方向行驶.经2时,船行驶至B处,此时灯塔C在B处的北偏西85°方向.已知灯塔C在A港的北偏西20°方向,则B,C两处的距离为________km.
如图,上午7:00,一船从A港出发,以20km/h的速度向东北方向行驶.经2时,船行驶至B处,此时灯塔C在B处的北偏西85°方向.已知灯塔C在A港的北偏西20°方向,则B,C两处的距离为________km.