Question

【题目】又到了一年中的春游季节．某班学生利用周末去参观“三军会师纪念塔”．下面是两位同学的一段对话：
甲：我站在此处看塔顶仰角为60°；
乙：我站在此处看塔顶仰角为30°；
甲：我们的身高都是1.6m；
乙：我们相距36m．
请你根据两位同学的对话，计算纪念塔的高度．（精确到1米）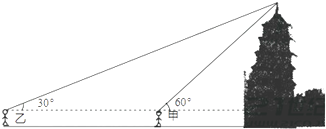

Answer 1

【答案】解：如图，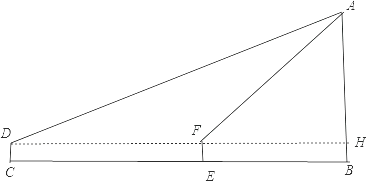

CD=EF=BH=1.6m，CE=DF=36m，∠ADH=30°，∠AFH=30°，
在Rt△AHF中，∵tan∠AFH= ，
∴FH= ，
在Rt△ADH中，∵tan∠ADH= ，
∴DH= ，
而DH﹣FH=DF，
∴ ﹣ =36，即 ﹣ =36，
∴AH=18 ，
∴AB=AH+BH=18 +1.6≈33（m）．
答：纪念塔的高度约为33m．
【解析】在Rt△AHF中,由∠AFH的正切可表示FH，在Rt△ADH中，由∠ADH的正切可表示DH，再根据DH﹣FH=DF，可得关于AH的方程，解这个方程得到AH的长，则根据AB的构成可求出AB的长。